Gjatesia e harkut te rrethit. Siperfaqja e sektorit qarkor

Gjatesia e harkut te rrethit

Gjatesia e harkut $\displaystyle {{1}^{\circ }}$

Përkufizim: “Këndi me kulm në qendrën e rrethit quhet kënd qendror”.

Masë në gradë të harkut,që pret këndin qëndror në rreth, do të quajmë masën në gradë të këndit qëndror.

Gjatesia e harkut $\displaystyle {{n}^{\circ }}$

Përkufizim: “Gjatësia $\displaystyle l$ e harkut prej $\displaystyle {{n}^{\circ }}$ të rrethit me rreze r jepet nga formula $\displaystyle l=\frac{\pi rn}{180}$ ”.

Ushtrimi 1

Shprehni në formulën më sipër:

a) r nëpërmjet l dhe n

b) n nëpërmjet r dhe n

Zgjidhje

a) Nga rregullat e veçimit të shkronjave në formulaa do të kemi:

$\displaystyle \pi rn=180\cdot l$

$\displaystyle r=\frac{180\cdot l}{\pi n}$

b) Nga rregullat e veçimit të shkronjave në formula do të kemi:

$\displaystyle \pi rn=180\cdot l$

$\displaystyle n=\frac{180\cdot l}{\pi r}$

Ushtrimi 2

Rrethi me rreze r = 2 cm, hapet duke formuar një hark rrethi me rreze R = 5 cm. Gjeni masën në gradë të këtij harku.

Zgjidhje

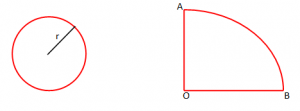
Perimetri i rrethit të dhënë është $\displaystyle P=2\pi r=4\pi$ .

Harku AB ka gjatësi të njëjtë me rrethin, pra $\displaystyle l=4\pi$ .

Duke shënuar me n masën në gradë të këtij harku, kemi $\displaystyle l=\frac{\pi Rn}{180}$ .

$\displaystyle 4\pi =\frac{\pi \cdot 5\cdot n}{180}$

$\displaystyle 5\pi n=720\pi$

$\displaystyle 5n=720$

$\displaystyle n=\frac{720}{5}={{144}^{\circ }}$ .

Siperfaqja e sektorit qarkor

Përkufizim: “Pjesa e qarkut që kufizohet nga dy rreze të tij quhet sektor qarku”.

Sipërfaqja e sektorit të qarkut të rrethit me rreze r dhe kënd qëndror $\displaystyle {{n}^{\circ }}$ është $\displaystyle S=\frac{\pi {{r}^{2}}n}{360}$ .

Ushtrimi 1

Në formulën më sipër:

a) Shprehni n nëpërmjet S dhe r.

a) Shprehni r nëpërmjet S dhe n.

Zgjidhje

a) Nga rregullat e veçimit të shkronjave në formula do të kemi:

$\displaystyle \pi {{r}^{2}}n=360\cdot S$

$\displaystyle {{r}^{2}}=\frac{360\cdot S}{\pi n}$

$\displaystyle r=\sqrt{\frac{360\cdot S}{\pi n}}$

b) Nga rregullat e veçimit të shkronjave në formula do të kemi:

$\displaystyle \pi {{r}^{2}}n=360\cdot S$

$\displaystyle n=\frac{360\cdot S}{\pi {{r}^{2}}}$

Rrjedhim: Formula $\displaystyle S=\frac{\pi {{r}^{2}}n}{360}$ mund të shkruhet ndryshe $\displaystyle S=\frac{1}{2}\left( \frac{\pi rn}{180} \right)\cdot r$ .

Duke ditur që $\displaystyle l=\frac{\pi rn}{180}$ , do të kemi:

$\displaystyle S=\frac{1}{2}\cdot l\cdot r$ .

Pra, themi: “Sipërfaqja e sektorit qarkor është e barabartë me gjysmën e prodhimit të rrezes me gjatësinë e harkut të sektorit”.