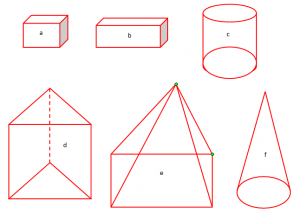
Trupat gjeometrike i kemi studiuar dhe në klasat e mëparshme, ku jemi njohur me prizmin, kubin, kuboidin, piramidën, cilindrin dhe konin.
Figurat më lartë janë trupa gjeometrike të cilat i kemi shënuar me gërma të vogëla.
- Figura a është një kub
- Figura b është një kuboid
- Figura c është një cilindër
- Figura d është një prizëm
- Figura e është një piramidë
- Figura f është një konë.
Këta janë trupa që nuk ndodhen në një plan. Ato zënë një vend të caktuar në hapësirë, veti të cilën nuk e kanë figura të tjera të njohura si trekëndëshi, drejtkëndëshi etj.
Pjesa e gjeometrisë që studion trupa të tillë quhet gjeometria në hapësirë.
Prizmi i drejtë
Prizëm i drejtë quhet shumëfaqëshi, i cili ka për baza dy shumëkëndësha kongruentë me brinjë përkatësisht paralele dhe faqet anësore i ka drejtkëndësha.
Prizmi i drejt katërkëndor, i cili ka bazën drejtkëndësh quhet kuboid. Të gjitha faqet e kuboidit janë drejtkëndësha.
Kub është kuboidi i cili ka të gjitha faqet katrora kongruentë.
Për trupat gjeometrike ndërtojmë tabelën më poshtë me numrin e faqeve, numrin e brinjëve dhe numrin e kulmeve të tyre.
| Shumëfaqëshi | Numri i faqeve | Numri i brinjëve | Numri i kulmeve |
| Kubi | 6 | 12 | 8 |
| Kuboidi | 6 | 12 | 8 |
| Prizmi trekëndor | 5 | 9 | 6 |
| Piramida trekëndore | 4 | 6 | 4 |
| Piramida katërkëndore | 5 | 8 | 5 |
Sipërfaqja e trupave gjeometrike
Në klasën e shtatë kemi llogaritur sipërfaqen e trupave gjeometrike.
- Kubi
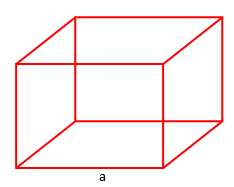
Të gjitha faqet e kubit janë me brinjë a. Sipërfaqja e secilës prej faqeve është .
Sipërfaqja e kubit është .
Shembull
Sipërfaqja e përgjithshme e kubit është . Gjeni brinjën e kubit
Zgjidhje
Nga formula, dimë që:
.
Bëjmë zëvëndësimet:
- Kuboidi
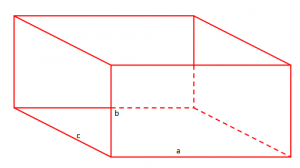
Të gjitha faqet e kuboidit janë drejtkëndësha.
Do të kemi: