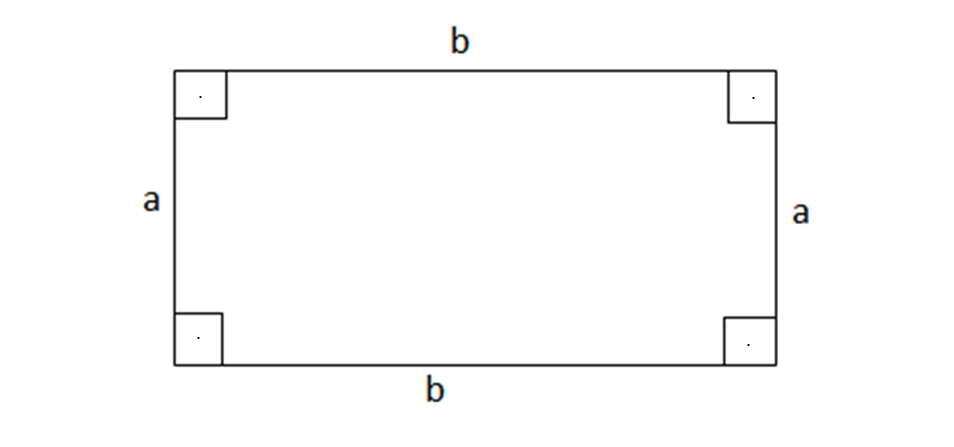
Drejtkendeshi | Vetite e drejtkendeshit | Perimetri dhe siperfaqja

Pasi mësuam paralelogramin, tani do mesojmë drejtkendeshin, vetite, perimetrin dhe siperfaqen e drejtkendeshit.

Përkufizim: “Drejtekëndësh quhet paralelogrami që i ka të katër këndet e drejta”.

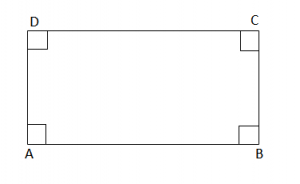
Drejtkendeshi

$\displaystyle \angle A=\angle B=\angle C=\angle D=90{}^\text{o}$

Vetite e drejtkendeshit

Vetia 1: “Drejtkëndëshi është paralelogram”.

Meqë është paralelogram, zotëron gjithë vetitë e paralelogramit që kemi përmendur ketu”.

Përveç këtyre vetive, drejtkendëshi ka dhe këto veti:

Vetia 2: “Diagonalet e drejtkendeshit janë kongruente”.

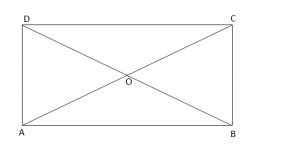
drejtkendeshi - diagonalet

AC = BD

Kushti që një katërkëndësh të jetë drejtkendesh është:

Kur diagonalet e tij janë kongruente dhe përgjysmojnë njëra-tjetrën.

Perimetri i drejtkendeshit

Perimetri i drejtkendeshit gjendet duke mbledhur gjitha brinjët e tij.

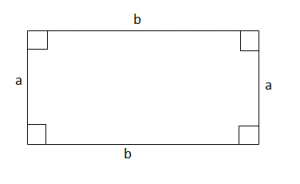
Pra, do të kemi:

P = a + b + a + b

P = 2a + 2b

P = 2 (a + b)

Shembull 1

Gjeni perimetrin e drejtkendeshit me gjatësi 10 cm dhe gjerësi 6 cm.

Zgjidhje

Kemi të dhënë:

a = 10 cm

b = 6 cm

P = ?

Nga formula e perimetrit dimë që:

P = 2a + 2b

P = 2 ∙ 10 + 2 ∙ 6

P = 20 + 12

P = 32 cm.

Përgjigje: Perimetri i drejtkëndeshit me gjatësi 10 cm dhe gjerësi 6 cm është 32 cm.

Shembull 2

Gjeni perimetrin e drejtkendeshit me gjatësi 12 cm dhe gjerësi sa gjysma e gjatësisë.

Zgjidhje

Kemi të dhënë:

a = 16 cm

$\displaystyle b=\frac{1}{2}a$

Në fillim gjejmë gjerësinë e drejtkëndeshit:

$\displaystyle b=\frac{1}{2}a$

$\displaystyle b=\frac{1}{2}\cdot 12$

$\displaystyle b=6$ cm

Nga formula e perimetrit dimë që:

P = 2a + 2b

P = 2 ∙ 12 + 2 ∙ 6

P = 24 + 12

P = 36 cm

Shembull 3

Gjeni gjerësinë e drejtkendeshit, kur dimë që perimetri i tij është 20 cm dhe gjatësia është 7 cm.

Zgjidhje

Kemi të dhënë:

P = 20 cm

a = 7 cm

b = ?

Nga formula e perimetrit dimë që:

P = 2a + 2b

Pra, do të kemi:

20 = 2 ∙ 7 + 2b

2b = 20 – 14

2b = 6

$\displaystyle b=\frac{6}{2}$

b = 3 cm.

Siperfaqja e drejtkendeshit

Siperfaqja e drejtkendeshit gjendet duke shumëzuar gjatësinë e tij me gjerësinë.

Pra, do të kemi:

S = a ∙ b

Shembull 1

Gjeni sipërfaqen e drejtkendeshit me gjatësi 16 cm dhe gjerësi 7 cm.

Zgjidhje

Nga formula e siperfaqes, dimë që:

S = a ∙ b

S = 16 ∙ 7

S = 112 $\displaystyle c{{m}^{2}}$ .

Shembull 2

Gjeni siperfaqen e drejtkendeshit me gjatësi 21 cm dhe gjerësi sa $\displaystyle \frac{1}{3}$ e gjatësisë.

Zgjidhje

Kemi të dhënë:

a = 21 cm

$\displaystyle b=\frac{1}{3}a$

S = ?

Në fillim gjejmë sa është gjerësia e drejtkëndeshit:

$\displaystyle b=\frac{1}{3}a$

$\displaystyle b=\frac{1}{3}\cdot 21$

b = 7 cm.

Tani gjejmë siperfaqen:

S = a ∙ b

S = 21 ∙ 7

S = 147 $\displaystyle c{{m}^{2}}$

Shembull 3

Gjeni brinjët e drejtkendeshit, kur dini sipërfaqen e tij $\displaystyle 100c{{m}^{2}}$ dhe gjerësia e tij sa $\displaystyle \frac{1}{4}$ e gjatësisë.

Zgjidhje

Kemi të dhënë:

$\displaystyle S=100c{{m}^{2}}$

$\displaystyle b=\frac{1}{4}a$

Nga formula e siperfaqes, dimë që:

S = a ∙ b

Bëjmë zëvëndësimet:

$\displaystyle 100=a\cdot \frac{1}{4}a$

$\displaystyle \frac{{{a}^{2}}}{4}=100$

$\displaystyle {{a}^{2}}=400$

$\displaystyle a=20$ cm

Tani gjejmë dhe brinjën b:

$\displaystyle b=\frac{1}{4}a$

$\displaystyle b=\frac{1}{4}\cdot 20$

$\displaystyle b=5$ cm