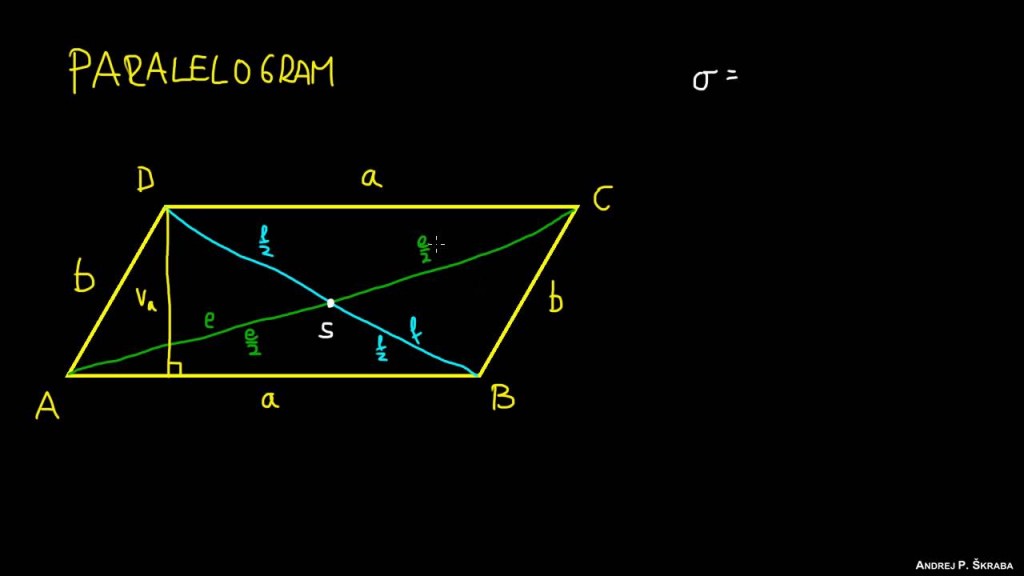
Paralelogrami

vetite e paralelogramit

Përkufizim: “Paralelogrami quhet katërkëndëshi që i ka brinjët dy nga dy paralele”.

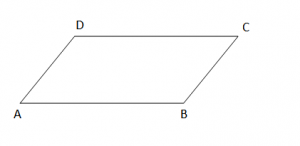
Paralelogrami

paralelogrami

AD // BC

AB // CD

Vetitë e paralelogramit

Vetia 1: “Në çdo paralelogram, brinjët paralele janë kongruente”.

paralelogrami

AD = BC

AB = CD

Vetia 2: “Në çdo paralelogram, këndet e kundërt janë kongruentë”.

paralelogrami

$\displaystyle \angle A=\angle C$

$\displaystyle \angle B=\angle D$

Vetia 3: “Në çdo paralelogram, diagonalet përgjysmojnë njëra tjetrën ”.

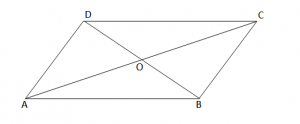
paralelogrami - diagonalet

AO = OC

BO = OD

Vetia 4: “Në çdo paralelogram, çdo dy kënde të njëpasnjëshëm e kanë shumën 180º”.

paralelogrami

$\displaystyle \angle A+\angle B=180{}^\text{o}$

$\displaystyle \angle B+\angle C=180{}^\text{o}$

$\displaystyle \angle C+\angle D=180{}^\text{o}$

$\displaystyle \angle D+\angle A=180{}^\text{o}$

Vetia 5: “Çdo diagonale e ndanë paralelogramin në dy trekëndësha kongruentë”.

paralelogrami - diagonalet

$\displaystyle \vartriangle ABC=\vartriangle ACD$

$\displaystyle \vartriangle ABD=\vartriangle BCD$

Vetia 6: “Diagonalet e ndajnë paralelogramin në katër trekëndësha, dy nga dy kongruentë”.

paralelogrami - diagonalet

$\displaystyle \vartriangle AOB=\vartriangle COD$

$\displaystyle \vartriangle AOD=\vartriangle BOC$

Kushtet kur një katërkëndësh është një paralelogram:

Kur katërkëndëshi i ka brinjët e kundërta kongruente, ai është paralelogram
ose:
Kur katërkëndëshi i ka këndet e kundërta kongruente, ai është paralelogram.
ose:
Kur në një katërkëndësh, diagonalet përgjysmojnë njëra-tjetrën, ai është paralelogram.
ose:
Kur në një katërkëndësh, dy nga brinjët e kundërta janë kongruente dhe paralele, ai është paralelogram.

Perimetri i paralelogramit

Perimetri i paralelogramit është shuma e brinjëve të tij.

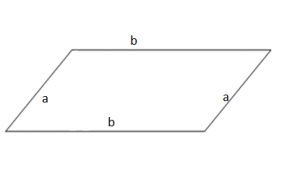
Pra, do të kemi:

P = a + b + a + b

P = 2a + 2b

P = 2(a + b).

Shembull 1

Gjeni perimetrin e paralelogramit me gjatësi 7 cm dhe gjerësi 4 cm.

Zgjidhje

Kemi të dhënë:

a = 7 cm

b = 4 cm

P = ?

Nga formula e perimetrit dimë që:

P = 2a + 2b

P = 2 ∙ 7 + 2 ∙ 4

P = 14 + 8

P = 22 cm.

Përgjigje: Perimetri i paralelogramit me gjatësi 7 cm dhe gjerësi 4 cm është 22 cm.

Shembull 2

Gjeni perimetrin e paralelogramit me gjatësi 16 cm dhe gjerësi sa gjysma e gjatësisë.

Zgjidhje

Kemi të dhënë:

a = 16 cm

$\displaystyle b=\frac{1}{2}a$

Nga formula e perimetrit dimë që:

P = 2a + 2b

Pra, do të kemi:

$\displaystyle P=2\cdot 16+2\cdot \left( \frac{1}{2}\cdot 16 \right)$

$\displaystyle P=32+16$

$\displaystyle P=48$ cm.

Shembull 3

Gjeni brinjët e paralelogramit, kur dimë që perimetri i tij është 24 cm dhe gjerësia është sa gjysma e gjatësisë.

Zgjidhje

Kemi të dhënë:

P = 24 cm

$\displaystyle b=\frac{1}{2}a$

Nga formula e perimetrit dimë që:

P = 2a + 2b

Pra, do të kemi:

$\displaystyle 24=2\cdot a+2\cdot \left( \frac{1}{2}\cdot a \right)$

$\displaystyle 2\cdot a+a=24$

$\displaystyle 3\cdot a=24$

$\displaystyle a=\frac{24}{3}$

$\displaystyle a=8$ cm.

Pra, kemi a = 8 cm. Tani gjejmë sa është gjerësia e tij:

$\displaystyle b=\frac{1}{2}a$

$\displaystyle b=\frac{1}{2}\cdot 8$

$\displaystyle b=4$ cm.

Siperfaqja e paralelogramit

Siperfaqja e paralelogramit gjendet duke shumëzuar bazën e tij me lartësinë e ndërtuar mbi të.

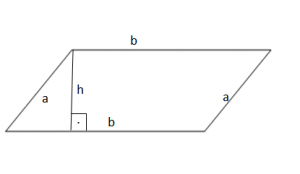
siperfaqja e paralelogramit

b – bazë e paralelogramit.

h – lartësia e ndërtuar mbi bazën.

Siperfaqja është: S = b ∙ h

Shembull 1

Gjeni siperfaqen e paralelogramit me gjatësi 12 cm dhe lartësi 5 cm.

Zgjidhje

Nga formula e paralelogramit,dimë që:

S = b ∙ h

Pra, do të kemi:

S = 12 ∙ 5

S = 60 $\displaystyle c{{m}^{2}}$

Shembull 2

Gjeni lartësinë e paralelogramit me gjatësi 8 cm dhe siperfaqe $\displaystyle 24c{{m}^{2}}$

Zgjidhje

Nga formula e paralelogramit, dimë që:

S = b ∙ h

Bejmë zëvëndësimet:

24 = 8 ∙ h

Duke zbatuar rregullat e vecimit te shkronjave ne formula, do të kemi:

$\displaystyle h=\frac{24}{8}$

$\displaystyle h=3$ cm

Postime te ngjashme: