Një figurë F ka qëndër simetrie pikën O, nëse të gjitha pikat e saj janë dy nga dy simetrike në lidhje me këtë pikë O në figurën F

 

Për shembull:

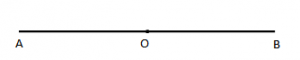
• Mesi i segmentit është qëndra e simetrisë e segmentit.

 

 

 

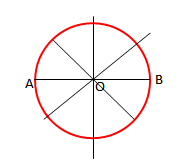
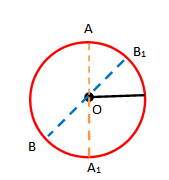
• Qëndra e rrethit është qëndër simetrie e rrethit.

 

• Çdo pikë e drejtëzës është qëndër simetrie e drejtëzës. Pra, drejtëza ka një pafundësi qëndrash simetrie

 

 

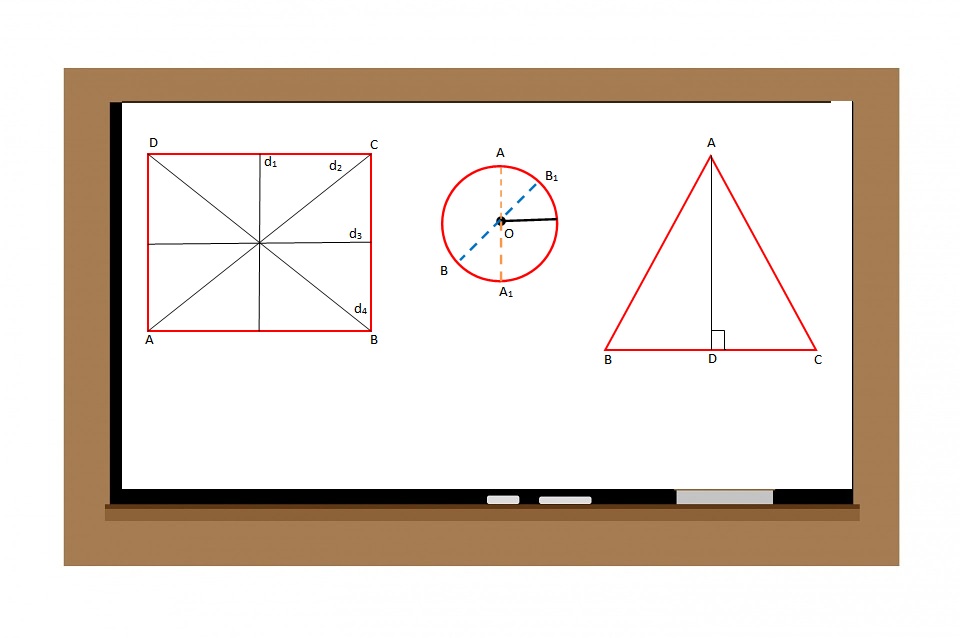
• Pika e prerjes së diagonaleve të katrorit është qëndër simetrie e katrorit.

 

 

 

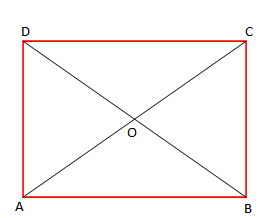
• Pika e prerjes së diagonaleve të drejtkendeshit është qëndër simetrie e drejtkëndëshit.

 

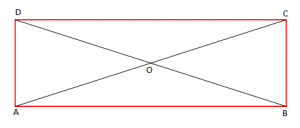
• Pika e prerjes së diagonaleve të paralelogramit është qëndër simetrie paralelogramit.

 

 

 

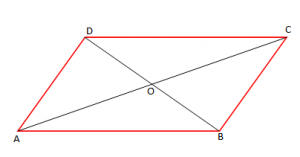
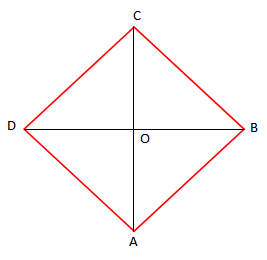
• Pika e prerjes së diagonaleve të rombit është qëndër simetrie e rombit.

 

• Pika e prerjes së diagonaleve të gjashtëkëndëshit të rregullt është qëndër simetrie e gjashtëkëndëshit të rregullt.

 

 

 

 

 

 

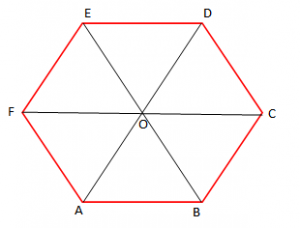
Simetria sipas një drejtëze

 

Simetrinë sipas një drejtëze e kemi studiuar në klasën e gjashte, tani do ta studiojmë më gjerë.

 

• Marrim një pikë K dhe një drejtëz a, që nuk kalon nga pika K.

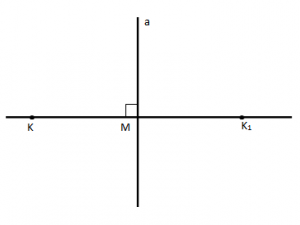
• Nga pika K ndërtojmë gjysmëdrejtëzën

 

• Marrim

 

• Pika quhet simetrike e pikës K në lidhje me drejtëzën a dhe anasjelltas, pika ka simetrike pikën K në lidhje me drejtëzën a.

 

• Nëse pika gjendet në drejtëz, ajo ka simetrike veten e saj. Pra, çdo pikë e nje drejtëze ka simetrike veten e saj. Drejtëza a quhet bosht simetrie.

 

 

 

 

 

Shembuj figurash që kanë bosht simetrie

• Përmesorja e segmentit është bosht simetrie i segmentit

 

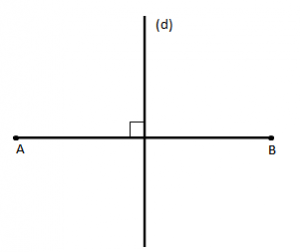
• Përgjysmorja e këndit është bosht simetrie i këndit.

 

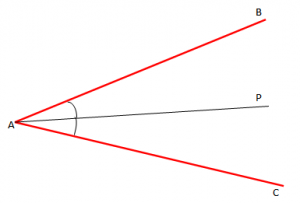
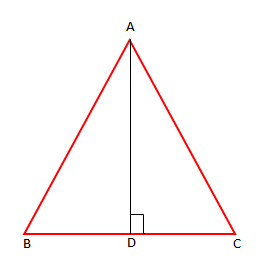
• Lartësia e trekëndëshit dybrinjëshëm është bosht simetrie i trekëndëshit dybrinjëshëm.

 

 

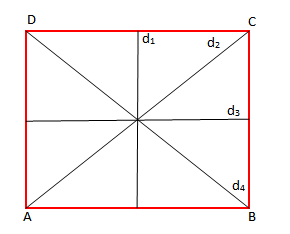
• Përmesoret e brinjëve të drejtkëndëshit janë boshte simetrie për të.

 

• Diagonalet e katrorit dhe përmesoret e brinjëve të tij janë boshte simetrie për të.

 

 

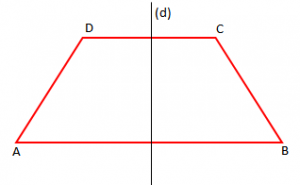
• Përmesorja e dy bazave të trapezit dybrinjëshëm është bosht simetrie për të.

 

 

• Çdo diametër i rrethit është bosht simetrie i tij.