
Siperfaqja. Kuptimi i siperfaqes
Kur bëjmë matjen e siperfaqes së figurës, ne e krahasojmë atë me një figurë tjetër, sipërfaqen e të cilës ne e marrim si njësi.
Si figurë e tillë merret zakonisht një katrorë me brinjë sa njësia e gjatësisë.
Aksioma IX
Duke zgjedhur një katror me brinjë sa njësia e gjatësisë, çdo figure i lidhet një numër, që quhet sipërfaqe e saj, në mënyrë që:
- Siperfaqja e çdo figure është një numër jonegativ.
- Siperfaqja e katrorit me brinjë sa njësia e gjatësisë është numri 1.
- Figura kongruente kanë sipërfaqe kongruente.
- Nëse një figurë është ndarë në pjesë që nuk priten, atëherë siperfaqja e saj është ë barabartë me shumën e sipërfaqeve të këtyre pjesëve.
Siperfaqja e drejtkëndëshit
Teoremë: “Siperfaqja e drejtkëndëshit me brinjë a dhe b është S = a ∙ b”.
Shembull 1
Të gjenden brinjët e drejtkendeshit, kur sipërfaqja është dhe gjatësia e tij është dyfishi i gjerësisë.
Zgjidhje
Nga ushtrimi kemi:
Shkruajmë formulën e siperfaqes së drejtkëndëshit:
.
Bëjmë zëvëndësimet:
Zgjidhim ekuacionin:
Tani gjejmë gjatësinë a:
Përgjigje: Brinjët e drejtkëndëshit janë: a = 20 cm dhe b = 10 cm.
Sipërfaqja e trekëndëshit
-
Sipërfaqja e trekëndëshit kënddrejt
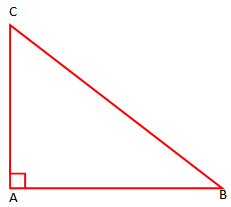
Teoremë: “Sipërfaqja e trekëndëshit kënddrejt është i barabartë me gjysmen e prodhimit të kateteve”.
Shembull 1
Gjeni katetet e trekëndëshit kënddrejt, nëse raporti i tyre është dhe sipërfaqja e tij është
.
Zgjidhje
Nga ushtrimi kemi:
Nga raporti i kateteve, nxjerrim a në dukje:
Shkruajmë formulën e siperfaqes së trekëndëshit kënddrejt:
Bëjmë zëvëndësimet:
Tani gjejmë katetin a:
- Siperfaqja e trekëndeshit çfarëdo
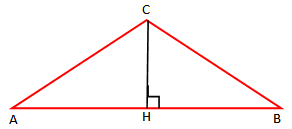
Teoremë: “Sipërfaqja e trekëndëshit është e barabartë me gjysmën e prodhimit të një brinje me lartësinë e hequr mbi të”.
Shembull 1
Gjeni sipërfaqen e trekëndëshit nëse njëra brinjë e trekëndëshit është 10 cm dhe lartësia e ndërtuar mbi këtë brinjë është 6 cm.
Zgjidhje
Nga ushtrimi kemi:
a = 10 cm
h = 6 cm
Shkruajmë formulën e siperfaqes së trekëndëshit:
Bëjmë zëvëndësimet:


