Trekendeshi kenddrejt | Veti te trekendeshit kenddrejt

Veti të trekëndëshit kenddrejt

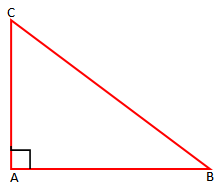
Përkufizim: “Trekëndëshi quhet i kenddrejt, nëse njëri nga këndet e tij është i drejt“.

Meqë shuma e këndeve të trekëndëshit është 180º, shuma e dy këndeve të tjera të trekëndëshit është 90º, pra janë kënde të ngusht.

Brinja e trekëndëshit që ndodhet përballë këndit të drejt quhet hipotenuzë, kurse dy brinjët e tjera quhen katete.

Teoremë 1: “Kateti i trekëndëshit kenddrejt që ndodhet perballë këndit 30º është sa gjysma e hipotenuzës”.

Teoremë 2 (e anasjellta e teoremës 1): “Nëse një katet i trekëndëshit kenddrejt është sa gjysma e hipotenuzës, atëherë këndi përballë këtij kateti është 30º”.

Ushtrimi 1

Gjeni këndet e trekëndëshit kenddrejt që është dybrinjëshëm.

Zgjidhje

Ndërtojmë trekëndëshin kenddrejt ABC.

Kemi:

AB = AC
$\displaystyle \hat{B}=\hat{C}$ nga vetia e trekëndëshit dybrinjëshëm.

Shënojmë me x këndet e bazës dhe formojmë ekuacionin:

$\displaystyle x+x+90=180$

$\displaystyle 2x=90$

$\displaystyle x=\frac{90}{2}$

$\displaystyle x=45{}^\text{o}$

Ushtrimi 2

Njëri nga këndet ë trekëndëshit kenddrejt është 60º, kurse hipotenuza është 12 cm. Gjeni gjatësinë e katetit të vogël të trekëndëshit.

Zgjidhje

Ndërtojmë trekëndëshin ABC.

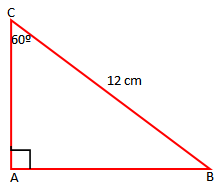
Në fillim gjejmë këndin tjetër të bazës.

Dimë që shuma e këndeve të ngusht tëk trekëndëshi kënddrejt është 90º, ndaj $\displaystyle \hat{B}=90-60=30{}^\text{o}$ .

Nga teorema, kemi që brinja që ndodhet përballë këndit 30º është sa gjysma e hipotenuzës.

Pra, $\displaystyle AC=\frac{1}{2}BC$

$\displaystyle AC=\frac{1}{2}\cdot 12=6cm$

Kongruenca e trekëndëshave kenddrejt

Teoremë: “Nëse katetet e një trekëndëshi kënddrejt janë përkatësisht kongruentë me katetet e një tjetër trekëndëshi kënddrejt, atëherë këta trekëndësha janë kongruentë”.

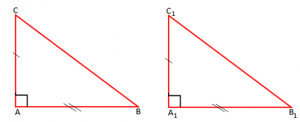
Vërtetim: Marrim në shqyrtim trekëndëshat ABC dhe $\displaystyle {{A}_{1}}{{B}_{1}}{{C}_{1}}$

Kemi:

$\displaystyle AC={{A}_{1}}{{C}_{1}}$
$\displaystyle AB={{A}_{1}}{{B}_{1}}$
$\displaystyle \hat{A}={{\hat{A}}_{1}}=90{}^\text{o}$

Nga rasti i dytë i kongruencës së trekëndëshave, kemi: $\displaystyle \vartriangle ABC=\vartriangle {{A}_{1}}{{B}_{1}}{{C}_{1}}$ .

Teoremë 2: “Nëse një katet dhe këndi i ngushtë pranë tij në një trekëndësh kënddrejt, janë përkatësisht kongruentë me një katet dhe këndin e ngushtë pranë tij në një tjetër trekëndësh kënddrejt, atëherë këta trekëndësha janë kongruentë”.

Teoremë 3: “Nëse hipotenuza dhe njëri kënd i ngushtë i një trekëndësh kënddrejt, janë përkatësisht kongruentë me hipotenuzën dhe njërin kënd të ngushtë të një tjetër trekëndëshi kënddrejt, atëherë këta trekëndësha janë kongruentë”.

Teoremë 4: “Nëse hipotenuza dhe njëri katet i një trekëndëshi kënddrejt, janë përkatësisht kongruentë me hipotenuzën dhe njërin katet të një tjetër trekëndëshi kënddrejt, atëherë këta trekëndësha janë kongruentë”.

Teoremat 2, 3 dhe 4 vërtetohen në të njëtën mënyrë si në rastin e teoremës 1.