Trekendeshi | Veti te trekendeshave | Trekendeshi dybrinjeshem

Lartësia e trekëndëshit

Mund të vërtetohet që nga një pikë e dhënë, hiqet një dhe vëtëm një pingule me një drejtëz të dhënë.

Shohim figurën:

Në figurën tonë, AM, BN dhe CP janë lartesitë e trekëndëshit ABC.

Mesorja dhe përgjysmorja e trekëndëshit

Përkufizim: “Segmenti që bashkon një kulm të trekëndëshit me mesin e brinjës përballë tij, quhet mesore e trekëndëshit”.

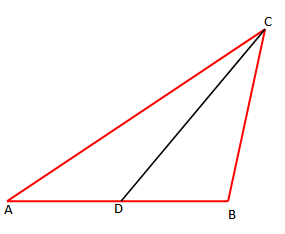
CD është mesore e trekëndëshit ABC, ku AD = DB.

Përkufizim: “Segmenti i përgjysmores së këndit të trekëndëshit, që bashkon kulmin e trekëndëshit me pikën e prerjes së saj me brinjën përballë, quhet përgjysmore e trekëndëshit”.

Trekendeshi dybrinjeshem. Veti te trekëndëshit dybrinjëshëm

Përkufizim: “Trekendeshi quhet dybrinjëshëm nëse ai ka dy brinjë kongruente”.

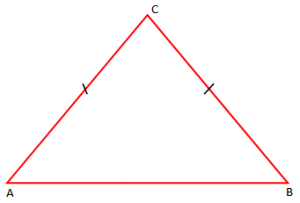
Tek trekendeshi dybrinjeshem, brinjët që janë kongruente quhën brinjë anësore.

Përkufizim: “Trekendeshi që i ka të tria brinjët e barabarta quhet trekëndësh barabrinjës”.

Teoremë 1: “Tek trekendeshi dybrinjeshem, këndet pranë bazës janë kongruente”.

Vërtetim. Le të jëtë trekëndëshi ABC një trekëndësh dybrinjëshëm. Kemi figurën:

Heqim përgjysmoren [CD] të dal nga kulmi C dhe do të kemi:

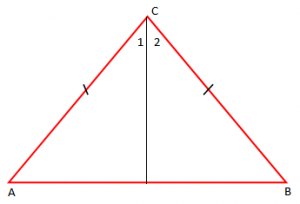
Trekëndëshat ACD dhe BCD janë kongruent në bazë të rastit të parë të kongruencës së trekëndëshave sepse:

$\displaystyle [AC]=[CB]$ si brinjë anësore të trekëndëshit dybrinjëshëm
$\displaystyle \hat{1}=\hat{2}$ , sepse [CD] është përgjysmore e këndit C
$\displaystyle [CD]$ brinjë e përbashkët e trekëndëshave ACD dhe BCD

Dimë që: “Në trekëndësha kongruentë, përballë brinjëve të barabarta ndodhen këndet e barabarta dhe anasjelltas”.

Përballë AC dhe BC kemi këndet C dhe C, ndaj $\displaystyle \angle A=B$ .

Teorema u vërtetua.

Teoremë 2 : “Në trekëndëshin dybrinjëshëm, mesorja e hequr nga kulmi ndaj bazës është edhe përgjysmore edhe lartësi e trekëndëshit”.

Ushtrimi 1

Në figurën më poshtë kemi $\displaystyle [AD]=[BD]$ dhe $\displaystyle \hat{1}=\hat{2}$ .

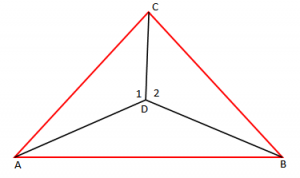
Vërtetoni që trekëndëshi ABC është trekëndësh dybrinjëshëm.

Zgjidhje

Marrim në shqyrtim $\displaystyle \vartriangle ACD$ dhe $\displaystyle \vartriangle BCD$

Kemi:

$\displaystyle AD=BD$
$\displaystyle \hat{1}=\hat{2}$
CD brinjë e përbashkët e dy trekëndëshave.

Në bazë të rastit të parë të kongruencës së trekëndëshave, kemi: $\displaystyle \vartriangle ACD=\vartriangle BCD$

Dimë që: “Në trekëndësha kongruentë, përballë brinjëve të barabarta ndodhen këndet e barabarta dhe anasjelltas”.

Përballë këndeve 1 dhe 2 ndodhen brinjët AC dhe BC, ndaj AC = BC.
Meqë brinjët anësore janë të barabarta, atëherë $\displaystyle \vartriangle ABC$ është dybrinjëshëm.