Izometria | Simetria qendrore, Simetria boshtore | Matematika 9

Izometria. Kuptimi i izometrisë

Pasqyrimi gjeometrik quhet izometri nëse largesa midis çdo dy pikave fytyrë është e njëjtë me largesën midis shëmbëllimeve të tyre.

Pra, pasqyrimi quhet izometri nëse për çdo dy pika A, B të planit, që kanë si shëmbëllimë pikat $\displaystyle {{A}_{1}}$ , $\displaystyle {{B}_{1}}$ ne kemi $\displaystyle {{A}_{1}}{{B}_{1}}=AB$ .

Fjala izometri vjen nga greqishtja e vjetër dhe do të thotë pikërisht “me gjatësi të barabartë”. Izometria është pasqyrimi gjeometrik që ruan formën dhe përmasën e figurës.

Veti të izometrisë

Teorema 1: “Pikat që ndodhen në një drejtëz, me anë të izometrisë kalojnë në pika që ndodhen përsëri në drejtëz, duke ruajtur renditjen”.

Rrjedhime të teoremës 1:

Nëse në izometrinë f, $\displaystyle A\to {{A}_{1}}$ dhe $\displaystyle B\to {{B}_{1}}$ , atëherë figura-shëmbëllim e [AB] është $\displaystyle [{{A}_{1}}{{B}_{1}}]$
Nëse në izometrinë f, $\displaystyle A\to {{A}_{1}}$ dhe $\displaystyle B\to {{B}_{1}}$ , atëherë figura-shëmbëllim e gjysmë drejtëzës [AB) është $\displaystyle [{{A}_{1}}{{B}_{1}})$
Nëse në izometrinë f, $\displaystyle A\to {{A}_{1}}$ , $\displaystyle B\to {{B}_{1}}$ dhe $\displaystyle C\to {{C}_{1}}$ , atëherë figura-shëmbëllim e këndit $\displaystyle A\hat{B}C$ është këndi $\displaystyle {{A}_{1}}{{\hat{B}}_{1}}{{C}_{1}}$

Teorema 2: “Izometria ruan masën e këndeve”.

Teoremë 3: “Shëmbëllimi i rrethit me qendër P e rreze r në një izometri është një rreth me të njejtën rreze e me qendër në shëmbëllimin e pikës O”.

Teoremat që pamë tregojnë se izometria është pasqyrim që ruan formën dhe përmasat e figurave.

Simetria qendrore

Përkufizim: “Simetri qendrore me qendër O quhet pasqyrimi që çdo pikë M të planit e lidh me pikën $\displaystyle {{M}_{1}}$ , të tillë që O të jetë mes i $\displaystyle \left[ M{{M}_{1}} \right]$ ”.

Veti të simetrisë qendrore

Teoremë: “Simetria qendrore me qendër O është izometri”.

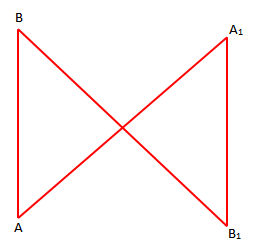
Rrjedhim: “Simetria qendrore gëzon të gjitha vetitë e njohura të izometrisë”.

Figura që kanë qendër simetrie

Nëse në simetrinë qendrore me qendër O, figura F ka si shëmbëllim veten, atëherë pika O quhet qendër simetrie e figurës F.

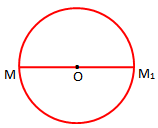
Për shembull, rrethi me qendër O dhe rreze r ka si qendër simetrie pikën O.

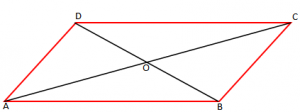
Teoremë: “Pika e prerjes së diagonaleve të paralelogramit është qendër simetrie e paralelogramit”.

Simetria boshtore

Përkufizim: “Simetri boshtore sipas drejtëzës d quhet pasqyrimi që çdo pikë M të planit M e kalon në pikën $\displaystyle {{M}_{1}}$ , të tillë që që drejtëza d të jetë përmesore e segmentit $\displaystyle [M{{M}_{1}}]$ ”.

Simetrinë boshtore sipas drejtëzës d e shënojmë shkurt $\displaystyle {{S}_{d}}$ .

Vetitë e simetrisë boshtore

Teoremë : “Simetria boshtore është izometri”.

Figura që kanë bosht simetrie

Përkufizim: “Nëse shëmbëllimi i çdo pike të figurës F në simetrinë sipas drejtëzës d është përsëri pikë e figurës F, atëherë d quhet bosht simetrie i figurës F“.

Për shembull, rrethi ka bosht simetrie.