Vlerat e funksioneve trigonometrike te kendeve 0º-90º

Funksionet trigonometrike te kendeve 30º; 45º dhe 60º

a) Në trekëndëshin kënddrejtë ABC jepen $\displaystyle \angle BAC=\alpha =30{}^\text{o}$ dhe $\displaystyle \angle ABC=\alpha =60{}^\text{o}$ .

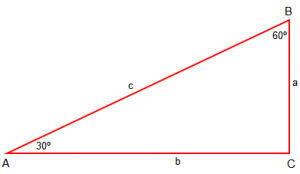
Kemi c= 2a, sepse ne dimë që kateti që ndodhet përballë këndit 30º është sa gjysma e hipotenuzës.

Me anë të teoremës së Pitagorës gjejmë:

$\displaystyle {{b}^{2}}={{c}^{2}}-{{a}^{2}}$

$\displaystyle {{b}^{2}}=4{{a}^{2}}-{{a}^{2}}=3{{a}^{2}}$

$\displaystyle b=\sqrt{3{{a}^{2}}}=a\sqrt{3}$ .

Tani gjejmë funksionet trigonometrike të këndit 30º.

$\displaystyle \sin 30{}^\text{o}=\frac{a}{c}=\frac{a}{2a}=\frac{1}{2}$ .

$\displaystyle \cos 30{}^\text{o}=\frac{b}{c}=\frac{a\sqrt{3}}{2a}=\frac{\sqrt{3}}{2}$ .

$\displaystyle tg30{}^\text{o}=\frac{a}{b}=\frac{a}{a\sqrt{3}}=\frac{\sqrt{3}}{3}$

$\displaystyle \cot30{}^\text{o}=\frac{b}{a}=\frac{a\sqrt{3}}{a}=\sqrt{3}$

Këndi $\displaystyle \beta$ është 60º dhe është plotësuesi i këndit 30º. Sipas varësisë së këndeve plotësuese shkruajmë:

$\displaystyle \sin 60{}^\text{o}=\cos 30{}^\text{o}=\frac{\sqrt{3}}{2}$

$\displaystyle \cos 60{}^\text{o}=\sin 30{}^\text{o}=\frac{1}{2}$

$\displaystyle tg60{}^\text{o}=\cot30=\sqrt{3}$

$\displaystyle \cot60{}^\text{o}=tg30{}^\text{o}=\frac{\sqrt{3}}{3}$ .

b) Në trekëndëshin kënddrejtë ABC jepen $\displaystyle \alpha =\beta =45{}^\text{o}$ .

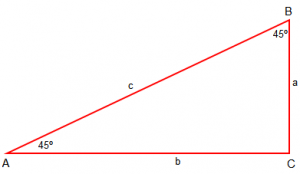
Trekëndëshi ABC është trekëndësh dybrinjëshëm sepse këndet në bazë janë të barabartë, pra b=a.

Me anë të teoremës së Pitagorës gjejmë hipotenuzën c:

$\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}=2{{a}^{2}}$

$\displaystyle c=\sqrt{2{{a}^{2}}}=a\sqrt{2}$

Tani gjejmë funksionet trigonometrike të këndit 45º.

$\displaystyle \sin {{45}^{\text{o}}}=\frac{a}{c}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$

$\displaystyle \cos 45{}^\text{o}=\frac{b}{c}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$

$\displaystyle tg45{}^\text{o}=\frac{a}{b}=\frac{a}{a}=1$

$\displaystyle cot45{}^\text{o}=\frac{b}{a}=\frac{a}{a}=1$

Përfundimet e gjetura i hedhim në tabelën e mëposhtme:

Këndi α	30º	45º	60º
sinα	$\displaystyle \frac{1}{2}$	$\displaystyle \frac{\sqrt{2}}{2}$	$\displaystyle \frac{\sqrt{3}}{2}$
cosα	$\displaystyle \frac{\sqrt{3}}{2}$	$\displaystyle \frac{\sqrt{2}}{2}$	$\displaystyle \frac{1}{3}$
tgα	$\displaystyle \frac{\sqrt{3}}{3}$	1	$\displaystyle \sqrt{3}$
cotgα	$\displaystyle \sqrt{3}$	1	$\displaystyle \frac{\sqrt{3}}{3}$

Varësia ndërmjet brinjëve dhe këndeve në trekëndëshin kënddrejtë

Nga përkufizimi i funksioneve trigonometrike kemi:

$\displaystyle sin\alpha =\frac{a}{c}\Rightarrow a=c\cdot sin\alpha$

$\displaystyle \cos a=\frac{b}{c}\Rightarrow b=c\cdot \cos \alpha$

$\displaystyle tga=\frac{a}{b}\Rightarrow b=a\cdot tg\alpha$

$\displaystyle cota=\frac{b}{a}\Rightarrow a=b\cdot cotga$

Pra, si përfundim ne mund të shkruajmë:

Përkufizim 1: “Në trekëndëshin kënddrejtë çdo katet është i barabartë me prodhimin e hipotenuzës me sinusin e këndit përballë këtij kateti”.

Përkufizim 2: “Në trekëndëshin kënddrejtë çdo katet është i barabartë me prodhimin e hipotenuzës me kosinusin e këndit të anëshkruar këtij kateti”.

Përkufizim 3: “Në trekëndëshin kënddrejtë çdo katet është i barabartë me prodhimin e katetit tjetër me tangentin e këndit përballë tij”.

Përkufizim 4: “Në trekëndëshin kënddrejtë çdo katet është i barabartë me prodhimin e katetit tjetër me kotangentin e këndit të anëshkruar tij”.

Këto barazime përdoren për të gjetur elementin e panjohur të trekëndëshit kënddrejtë kur jepen dy elemente të tij (të paktën njëri prej tyre duhet të jetë brinjë).