Paralelogrami, drejtkendeshi, rombi, katrori | Teorema e Talesit

Paralelogrami, drejkendeshi, rombi dhe katrori janë trajtuar edhe në klasën e gjashtë, tek mësimi Shumekendeshat

Paralelogrami

Përkufizim: “Paralelogram quhet katërkëndëshi që i ka brinjët dy nga dy paralele”.

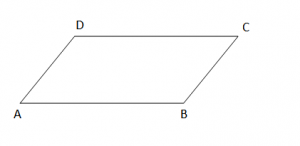
paralelogrami

AD // BC

AB // CD

Vetitë e paralelogramit

Vetia 1: “Në çdo paralelogram, brinjët paralele janë kongruente”.

paralelogrami

AD = BC

AB = CD

Vetia 2: “Në çdo paralelogram, këndet e kundërt janë kongruentë”.

paralelogrami

$\displaystyle \angle A=\angle C$

$\displaystyle \angle B=\angle D$

Vetia 3: “Në çdo paralelogram,diagonalet përgjysmojnë njëra tjetrën ”.

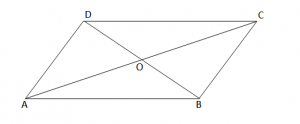
AO = OC

BO = OD

Vetia 4: “Në çdo paralelogram, çdo dy kënde të njëpasnjëshëm e kanë shumën 180º”.

$\displaystyle \angle A+\angle B=180{}^\text{o}$

$\displaystyle \angle B+\angle C=180{}^\text{o}$

$\displaystyle \angle C+\angle D=180{}^\text{o}$

$\displaystyle \angle D+\angle A=180{}^\text{o}$

Vetia 5: “Çdo diagonale e ndanë paralelogramin në dy trekëndësha kongruentë”.

paralelogrami - diagonalet

$\displaystyle \vartriangle ABC=\vartriangle ACD$

$\displaystyle \vartriangle ABD=\vartriangle BCD$

Vetia 6: “Diagonalet e ndajnë paralelogramin në katër trekëndësha, dy nga dy kongruentë”.

paralelogrami - diagonalet

$\displaystyle \vartriangle AOB=\vartriangle COD$

$\displaystyle \vartriangle AOD=\vartriangle BOC$

Kushtet kur një katërkëndësh është një paralelogram:

Kur katërkëndëshi i ka brinjët e kundërta kongruente, ai është paralelogram
ose:
Kur katërkëndëshi i ka këndet e kundërta kongruente, ai është paralelogram.
ose:
Kur në një katërkëndësh, diagonalet përgjysmojnë njëra-tjetrën, ai është paralelogram.
ose:
Kur në një katërkëndësh, dy nga brinjët e kundërta janë kongruente dhe paralele, ai është paralelogram.

Për më shumë mbi paralelogramin: vetitë, perimetrin dhe siperfaqen e tij, klikoni Paralelogrami

Drejtkendeshi

Përkufizim: “Drejtekëndësh quhet paralelogrami që i ka të katër këndet e drejta”.

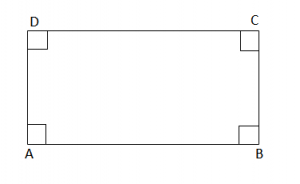
Drejtkendeshi

$\displaystyle \angle A=\angle B=\angle C=\angle D=90{}^\text{o}$

Vetitë e drejtkëndëshit

Vetia 1: “Drejtkëndëshi është paralelogram”.

Meqë është paralelogram, zotëron gjithë vetitë e paralelogramit që përmëndëm më sipër”.

Përveç këtyre vetive, drejtkendëshi ka dhe këto veti:

Vetia 2: “Diagonalet e drejtkendeshit janë kongruente”.

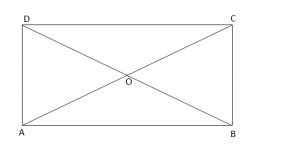
drejtkendeshi - diagonalet

AC = BD

Kushti që një katërkëndësh të jetë drejtkendesh është:

Kur diagonalet e tij janë kongruente dhe përgjysmojnë njëra-tjetrën.

Për më shumë mbi drejtkëndëshin (perimetri dhe siperfaqja e drejtkëndëshit) klikoni ketu

Rombi

Përkufizim: “Romb quhet paralelogrami që i ka të katër brinjët kongruente”.

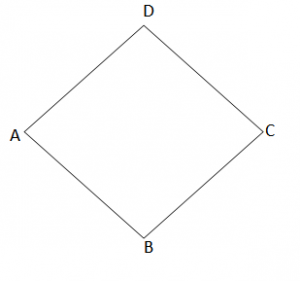
Rombi

AB = BC = CD = DA

Rombi është paralelogram dhe zotëron gjithe vetitë e tij që përmendëm më lart dhe ka këto veti të tjera:

Vetia 1: “Rombi i ka diagonalet pingule ndërmjet tyre”.

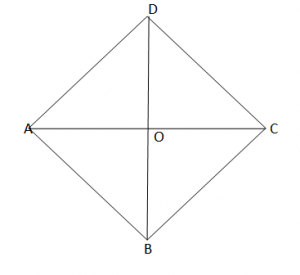
ROMBI-DIAGONALET

$\displaystyle AC\bot BD$

Vetia 2: “Rombi i ka diagonalet përgjysmore të këndeve të tij”.

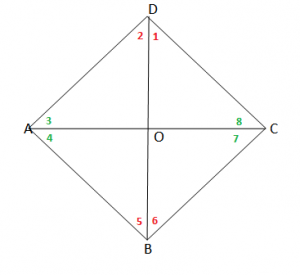
ROMBI-DIAGONALET-pergjysmojne

$\displaystyle \angle 1=\angle 2=\angle 5=\angle 6$

$\displaystyle \angle 3=\angle 4=\angle 7=\angle 8$

Vetia 3: “Diagonalet e rombit, e ndajnë rombin në katër trekëndësha kongruentë”.

ROMBI-DIAGONALET

$\displaystyle \vartriangle AOB=\vartriangle BOC=\vartriangle COD=\vartriangle DOA$

Kushtet që një paralelogram të jetë romb:

Kur diagonalet e tij janë pingule.
Kur njëra nga diagonalet e tij të përgjysmoj njërin kënd.

Për më shumë mbi rombin (perimetri dhe siperfaqj), klikoni ketu

Katrori

Përkufizim: “Katror quhet paralelogrami që i ka të katër brinjët kongruente dhe të katër këndet kongruente”.

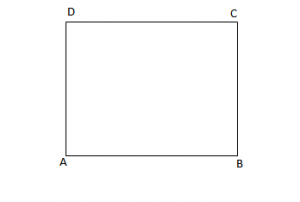
Katrori

AB = BC = CD = DA

$\displaystyle \angle A=\angle B=\angle C=\angle D$

Katrori, është paralelogram, është drejtkëndësh, është romb.

Katrori i ka të gjitha vetitë e figurave që përmëndëm më lart.

Katrori ka dhe këto veti:

Vetia 1: “Diagonalet e katrorit janë kongruente”.

Vetia 2: “Diagonalet e katrorit janë pingule”.

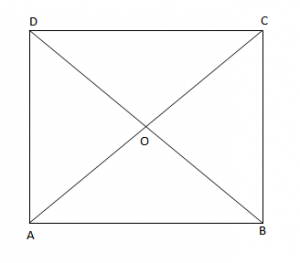
KATRORI-DIAGONALET

AC = BD

$\displaystyle AC\bot BD$

Vetia 3: “Diagonalet e katrorit janëpërgjysmore të këndeve të tij”.

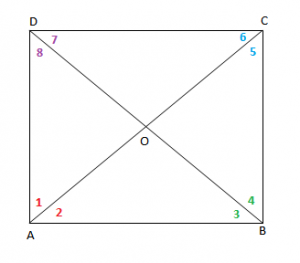
KATRORI-DIAGONALET-KENDET

$\displaystyle \angle 1=\angle 2$

$\displaystyle \angle 3=\angle 2=4$

$\displaystyle \angle 5=\angle 6$

$\displaystyle \angle 7=\angle 8$

Kushti që një paralelogram të jetë katror:

Kur diagonalet janë kongruente dhe pingule.
Kur diagonalet janë kongruente dhe njëra diagonale përgjysmon njërin kënd të tij.

Për më shumë mbi katrorin (perimetri dhe siperfaqja), klikoni ketu

Teorema e Talesit

Përkufizim: “Kur dy drejtëza paralele ndërmjet tyre presin dy drejtëza, atëherë ”segmentet e formuar në njërën drejtëz janë përpjestimorë me segmentet përkatëse në drejtëzën tjetër”.

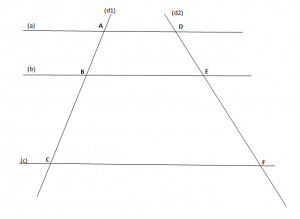
Teorema e Talesit

Kushti:

a // b // c
$\displaystyle {{d}_{1}}$ dhe $\displaystyle {{d}_{2}}$ prerëse të tyre.

Përfundimi:

$\displaystyle \frac{AB}{BC}=\frac{DE}{EF}$

$\displaystyle \frac{AC}{AB}=\frac{DF}{DE}$

$\displaystyle \frac{AC}{BC}=\frac{DF}{EF}$

Është e vërtetë dhe teorema e anasjelltë: “Kur dy drejtëza priten nga disa drejtëza dhe raporti i dy segmenteve çfarëdo në njërën drejtëz është i barabartë me raportin e dy segmenteve përkatës në drejtëzën tjetër, atëherë drejtëzat që presin dy drejtëzat janë paralele ndërmjet tyre”.

Vija e mesme e trekëndëshit

Përkufizim: “Segmenti që bashkon meset e dy brinjëve të trekëndëshit, quhet vijë e mesme e trekëndëshit”.

Teoremë: “Vija e mesme e trekëndëshit është paralele me brinjën e tretë të trekëndëshit dhe është sa gjysma e saj”.

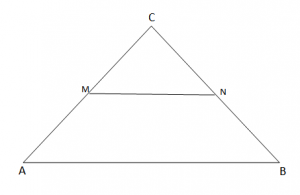
Vija e mesme e trekendeshit

Kushti:

MN – Vijë e mesme e $\displaystyle \vartriangle ABC$

Përfundimi:

MN || AB
$\displaystyle MN=\frac{1}{2}AB$