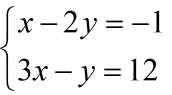Zgjidhja e sistemeve me mënyrën e zëvëndësimit
Zgjidhja e sistemeve me mënyrën e zëvëndësimit bëhet duke ndjekur këto hapa:
- Shprehim në ndonjë ekuacion njërën ndryshore nëpërmjet tjetrës.
- E zëvëndësojmë shprehjen e gjetur në vend të kësaj ndryshore në ekuacionin tjetër.
- E zgjidhim ekuacionin me një ndryshore që përftohet.
- Gjejmë vlerën përgjegjëse të ndryshores tjetër.
- Shkruajmë zgjidhjen e sistemit.
Shembull
Zgjidhni sistemin:
a) Duke veçuar ndryshoren x në ekuacionin e parë.
b) Duke veçuar ndryshoren y në ekuacionin e dytë.
Zgjidhje
a)
Tani zëvëndësojmë x tek ekuacioni i parë:
Tani zëvëndësojmë vlerën e y tek ekuacioni i parë dhe zgjidhim ekuacionin:
Përgjigje: Zgjidhje e sistemit është çifti i radhitur (3, 5).
b)
Tani zëvëndësojmë y tek ekuacioni i dytë:
Tani zëvëndësojmë vlerën e x tek ekuacioni I dytë dhe zgjidhim ekuacionin:
Përgjigje: Zgjidhje e sistemit është çifti i radhitur (3, 5).
Zgjidhja e sistemeve me mënyrën e mbledhjes
Zgjidhja e sistemeve me mënyrën e mbledhjes bëhet duke ndjekur këto hapa:
- Shumëzojmë secilin ekuacion anë për anë me numra të tillë që koeficientët pranë njërës ndryshore në të dy ekuacionet të bëhen numra të kundërt.
- Mbledhim anë për anë ekuacionet që formohen.
- Zgjidhim ekuacionin me një ndryshore që formohet.
- Gjejmë vlerën përgjegjëse të ndryshores tjetër duke zëvëndësuar në njërin nga ekuacionet.
- Shkruajmë zgjidhjen e sistemit.
Shembull
Zgjidhni me mënyrën e mbledhjes sistemin më poshtë:
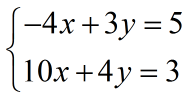
Zgjidhje
Në fillim shumëzojmë me 5 ekuacionin e parë dhe me 2 ekuacionin e dytë, në mënyrë që të zhdukim x-in nga sistemi:
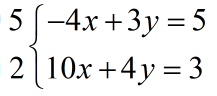
Tani do të kemi:
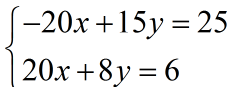
Tani kryejmë mbledhjen:
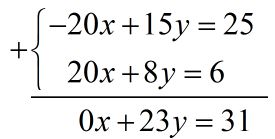
Tani zgjidhim ekuacionin që u përftua:
Tani zëvëndësojmë y tek njëri nga ekuacionet e sistemit. E zëvëndësojmë tek ekuacioni i parë: