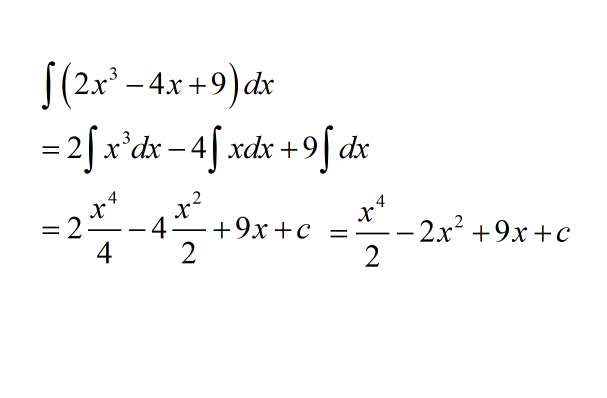
Ushtrime – Integrali i pacaktuar | Metoda e integrimit me pjese

Për zgjidhjen e ketyre ushtrimeve bazohemi tek 2 temat e integrali te pacaktuar:

Ushtrimi 1

Duke përdorur tabelën e integraleve themelore, të njehsohen integralet:

a) $\displaystyle \int{\left( 2{{x}^{3}}-4x+9 \right)dx}$

b) $\displaystyle \int{\left( {{2}^{x}}-3{{e}^{x}} \right)dx}$

c) $\displaystyle \int{\left( 2\sin x+4\cos x \right)dx}$

Zgjidhje

a) $\displaystyle \int{\left( 2{{x}^{3}}-4x+9 \right)dx}$

$\displaystyle =2\int{{{x}^{3}}}dx-4\int{xdx+9\int{dx}}$

$\displaystyle =2\frac{{{x}^{4}}}{4}-4\frac{{{x}^{2}}}{2}+9x+c$

$\displaystyle =\frac{{{x}^{4}}}{2}-2{{x}^{2}}+9x+c$

b) $\displaystyle \int{\left( {{2}^{x}}-3{{e}^{x}} \right)dx}$

$\displaystyle =\int{{{2}^{x}}dx-3\int{{{e}^{x}}}}dx$

$\displaystyle =\frac{{{2}^{x}}}{\ln 2}-3{{e}^{x}}+c$

c) $\displaystyle \int{\left( 2\sin x+4\cos x \right)dx}$

$\displaystyle =2\int{\sin xdx+4\int{\cos xdx}}$

$\displaystyle =-2\cos xdx+4\sin xdx+c$

$\displaystyle =4\sin xdx-2\cos xdx+c$

Ushtrimi 2

Të njehsohen integralet:

a) $\displaystyle \int{\left( 3-x \right)\left( 3+x \right)dx}$

b) $\displaystyle \int{\frac{\left( x-1 \right)\left( x+1 \right)}{x}dx}$

c) $\displaystyle \int{\frac{{{x}^{2}}-1}{x+1}dx}$

Zgjidhje

a) $\displaystyle \int{\left( 3-x \right)\left( 3+x \right)dx}$

Zbatojmë formulën e diferencës së katrorëve:

$\displaystyle =\int{\left( 9-{{x}^{2}} \right)dx}$

$\displaystyle =9\int{dx-\int{{{x}^{2}}dx}}$

$\displaystyle =9x-\frac{{{x}^{3}}}{3}+c$

b) $\displaystyle \int{\frac{\left( x-1 \right)\left( x+1 \right)}{x}dx}$

$\displaystyle =\int{\frac{{{x}^{2}}-1}{x}dx}$

$\displaystyle =\int{\frac{{{x}^{2}}-1}{x}dx}=\int{xdx-\int{\frac{dx}{x}}}$

$\displaystyle =\frac{{{x}^{2}}}{2}-\ln |x|+c$

c) $\displaystyle \int{\frac{{{x}^{2}}-1}{x+1}dx}$

$\displaystyle =\int{\frac{\left( x-1 \right)\left( x+1 \right)}{x+1}dx}=\int{\left( x-1 \right)dx}$

$\displaystyle =\frac{{{x}^{2}}}{2}-x+c$

Ushtrimi 3

Të njehsohen integralet:

a) $\displaystyle \int{\frac{7{{x}^{4}}-3{{x}^{2}}+4x}{{{x}^{2}}}dx}$

b) $\displaystyle \int{\frac{{{x}^{4}}+2{{x}^{2}}-1}{3x}dx}$

Zgjidhje

a) $\displaystyle \int{\frac{7{{x}^{4}}-3{{x}^{2}}+4x}{{{x}^{2}}}dx}$

$\displaystyle =7\int{{{x}^{2}}dx-3\int{dx+4\int{\frac{dx}{x}}}}$

$\displaystyle =7\frac{{{x}^{3}}}{3}-3x+4\ln |x|+c$

b) $\displaystyle \int{\frac{{{x}^{4}}+2{{x}^{2}}-1}{3x}dx}$

$\displaystyle =\frac{1}{3}\int{{{x}^{3}}+\frac{2}{3}\int{xdx-\frac{1}{3}\int{\frac{dx}{x}}}}$

$\displaystyle =\frac{1}{3}\cdot \frac{{{x}^{4}}}{4}+\frac{2}{3}\cdot \frac{{{x}^{2}}}{3}-\frac{1}{3}\cdot \ln |x|+c$

$\displaystyle =\frac{{{x}^{4}}}{12}+\frac{2{{x}^{2}}}{9}-\frac{\ln |x|}{3}+c$

Ushtrimi 4

Të njehsohen integralet duke përdorur metodën e integrimit me pjesë:

a) $\displaystyle \int{\left( x+1 \right)\cdot {{e}^{x}}dx}$

b) $\displaystyle \int{\left( 4x-3 \right)\cdot {{e}^{x}}dx}$

c) $\displaystyle \int{\left( x+1 \right)\cdot \sin xdx}$

d) $\displaystyle \int{{{x}^{3}}\cdot \ln xdx}$

e) $\displaystyle \int{\left( x+1 \right)\cdot \ln xdx}$

f) $\displaystyle \int{\sqrt{x}\cdot \ln xdx}$

Zgjidhje

a) $\displaystyle \int{\left( x+1 \right)\cdot {{e}^{x}}dx}$

Për të zgjidhur integralet me metodën e integrimit me pjesë shkruajmë:

$\displaystyle u=x+1$

$\displaystyle du=dx$

$\displaystyle dv={{e}^{x}}dx$

$\displaystyle v=\int{{{e}^{x}}dx={{e}^{x}}}$

Tani përdorim formuën e integrimit me pjesë:

$\displaystyle \int{udv}=uv-\int{vdu}$

$\displaystyle \left( x+1 \right)\cdot {{e}^{x}}-\int{{{e}^{x}}dx}$

$\displaystyle \left( x+1 \right)\cdot {{e}^{x}}-{{e}^{x}}+c$

$\displaystyle =x{{e}^{x}}+c$

b) $\displaystyle \int{\left( 4x-3 \right)\cdot {{e}^{x}}dx}$

Shkruajmë:

$\displaystyle u=4x-3$

$\displaystyle du=4dx$

$\displaystyle dv={{e}^{x}}dx$

$\displaystyle v=\int{{{e}^{x}}dx={{e}^{x}}}$

Zbatojmë formulën e integrimit me pjesë:

$\displaystyle \int{udv}=uv-\int{vdu}$

$\displaystyle \left( 4x-3 \right)\cdot {{e}^{x}}-\int{{{e}^{x}}}\cdot 4dx$

$\displaystyle =\left( 4x-3 \right)\cdot {{e}^{x}}-4{{e}^{x}}+c$

$\displaystyle ={{e}^{x}}\left( 4x-3-4 \right)+c$

$\displaystyle ={{e}^{x}}\left( 4x-1 \right)+c$

c) $\displaystyle \int{\left( x+1 \right)\cdot \sin xdx}$

shkruajmë:

$\displaystyle u=x+1$

$\displaystyle du=dx$

$\displaystyle dv=\sin xdx$

$\displaystyle v=\int{\sin xdx=-\cos x}$

Zbatojmë formulën e integrimit me pjesë:

$\displaystyle \int{udv}=uv-\int{vdu}$

$\displaystyle -\left( x+1 \right)\cdot \cos x-\int{-\cos xdx}$

$\displaystyle =-\left( x+1 \right)\cdot \cos x+\sin x+c$

$\displaystyle =\sin x-\left( x+1 \right)\cdot \cos x+c$

d) $\displaystyle \int{{{x}^{3}}\cdot \ln xdx}$

Shkruajmë:

$\displaystyle u=\ln x$

$\displaystyle du=\frac{dx}{x}$

$\displaystyle dv={{x}^{3}}dx$

$\displaystyle v=\int{{{x}^{3}}dx=\frac{{{x}^{4}}}{4}}$

Zbatojmë formulën e integrimit me pjesë:

$\displaystyle \int{udv}=uv-\int{vdu}$

$\displaystyle \ln x\cdot \frac{{{x}^{4}}}{4}-\int{\frac{{{x}^{4}}}{4}}\cdot \frac{dx}{x}$

$\displaystyle =\frac{{{x}^{4}}\cdot \ln x}{4}-\frac{1}{4}\int{{{x}^{3}}dx}$

$\displaystyle =\frac{{{x}^{4}}\cdot \ln x}{4}-\frac{1}{4}\cdot \frac{{{x}^{4}}}{4}+c$

$\displaystyle =\frac{3{{x}^{4}}\cdot \ln x}{16}+c$

e) $\displaystyle \int{\left( x+1 \right)\cdot \ln xdx}$

Shkruajmë:

$\displaystyle u=\ln x$

$\displaystyle du=\frac{dx}{x}$

$\displaystyle dv=\left( x+1 \right)dx$

$\displaystyle v=\int{\left( x+1 \right)dx=\frac{{{x}^{2}}}{2}+x}$

Zbatojmë formulën e integrimit me pjesë:

$\displaystyle \int{udv}=uv-\int{vdu}$

$\displaystyle \ln x\left( \frac{{{x}^{2}}}{2}+x \right)-\int{\left( \frac{{{x}^{2}}}{2}+x \right)}\frac{dx}{x}$

$\displaystyle =\ln x\cdot \left( \frac{{{x}^{2}}}{2}+x \right)-\int{\frac{{{x}^{2}}+2x}{2x}}dx$

$\displaystyle =\ln x\cdot \left( \frac{{{x}^{2}}}{2}+x \right)-\frac{1}{2}\cdot \frac{{{x}^{2}}}{2}+\frac{{{x}^{2}}}{2}+c$

$\displaystyle =\ln x\cdot \left( \frac{{{x}^{2}}}{2}+x \right)-\frac{{{x}^{2}}}{4}+\frac{{{x}^{2}}}{2}+c$

f) $\displaystyle \int{\sqrt{x}\cdot \ln xdx}$

Shkruajmë:

$\displaystyle u=\ln x$

$\displaystyle du=\frac{dx}{x}$

$\displaystyle dv=\sqrt{x}dx$

$\displaystyle v=\int{\sqrt{x}dx=\frac{{{x}^{\frac{3}{2}}}}{\frac{3}{2}}=\frac{2}{3}{{x}^{\frac{3}{2}}}}$

Zbatojmë formulën e integrimit me pjesë:

$\displaystyle \int{udv}=uv-\int{vdu}$

$\displaystyle \ln x\cdot \frac{2}{3}{{x}^{\frac{3}{2}}}-\int{\frac{2}{3}{{x}^{\frac{3}{2}}}}\cdot \frac{dx}{x}$

$\displaystyle =\frac{2}{3}\ln x\cdot {{x}^{\frac{3}{2}}}-\frac{2}{3}\int{{{x}^{\frac{1}{2}}}}dx$

$\displaystyle =\frac{2}{3}\ln x\cdot {{x}^{\frac{3}{2}}}-\frac{2}{3}\cdot \frac{2}{3}{{x}^{\frac{3}{2}}}$

$\displaystyle =\frac{2}{3}{{x}^{\frac{3}{2}}}\left( \ln x-\frac{2}{3} \right)$

Për zgjidhjen e ketyre ushtrimeve bazohemi tek 2 temat e integrali te pacaktuar:

Integrali i pacaktuar

Ushtrimi 1

Zgjidhje

Ushtrimi 2

Zgjidhje

Ushtrimi 3

Zgjidhje

Ushtrimi 4

Zgjidhje

Zbatojmë formulën e integrimit me pjesë:

Postime te ngjashme: