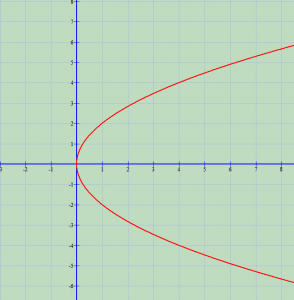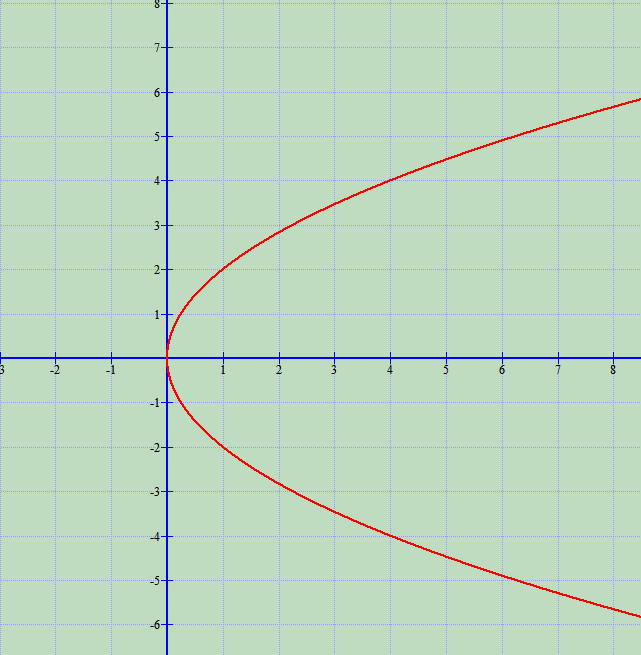
Parabola simetrike në lidhje me boshtin e abshisave
Parabolë quhet bashkësia e pikave të planit të baraslarguar nga një drejtëz fikse dhe nga një pikë e planit, jashtë kësaj drejtëze.
Drejtëza fikse PQ quhet vijë drejtuese , ndërsa pika fikse F quhet vatër e parabolës. Largesa FA e vatrës nga vija drejtuese shënohet me p dhe quhet parametër i parabolës.
Ky është vizatimi i parabolës në lidhje me boshtin e abshisave.
Për të nxjerr ekuacionin e parabolës, zgjedhim si origjinë të koordinatave mesin O të segmentit AF, ndërsa si bosht abshisash zgjedhim drejtëzën që kalon nga vatra F dhe është pingule me vijën drejtuese. Kemi .
Ekuacioni më i thjeshtë i parabolës është , ku p është parametër i parabolës.
Nëse vatra ndodhet majtas vijës drejtuese kemi dhe ekuacioni i parabolës është
.
Në qfotë se pika ndodhet në parabolë, koordinatat e saj vërtetojnë ekuacionin. Anasjelltas, çdo pikë, koordinatat e të cilës vërtetojnë ekuacionin ndodhet në parabolë.
Forma e parabolës
- Simetria
Parabola është vijë simetrike në lidhje me boshtin e abshisave. Boshti i abshisave quhet bosht i parabolës.
- Zona e vendosjes
Të gjitha pikat e parabolës ndodhen djathtas boshtit të ordinatave.
- Pikat e prerjes me boshtet
Për x=0 kemi y=0, që tregon s parabola kalon nga origjina e koordinatave. Pika quhet kulm i parabolës.
- Forma e parabolës
Me rritjen e vlerave të x nga 0 në kemi rritjen e vlerave të y nga 0 në
. Në këtë mënyrë forma e parabolës paraqitet sin ë figurë:
Shembull 1
Të shkruhet ekuacioni i parabolës me qendër në origjinën e koordinatave, simetrike në lidhje me boshtin e abshisave, me vijë drejtuese me ekuacion dhe vatër
.
Zgjidhje
Koordinatat e vatrës janë . Nga kushti shkruajmë:
.
Pra, ekuacioni i parabolës është:
Parabola simetrike në lidhje me boshtin e ordinatave
Në këtë rast OF e zgjedhim si bosht të ordinatave, ndërsa si origjinë të koordinatave zgjedhim përsëri mesin O. Kemi .
Ekuacioni më i thjeshtë i parabolës në lidhje me boshtin e ordinatave është .
Vija drejtuese PQ e kësaj parabole ka ekuacionin .
Nëse si drejtim të boshtit të ordinatave zgjedhim drejtimin nga F në O, atëherë parabola do të ketë ekuacionin dhe vija drejtuese e saj ka ekuacionin
.
Shembull 2
Të shkruhet ekuacioni i parabolës, me kulm në qendrën e ordinatave, simetrike në lidhje me boshti n e ordinatave në qoftë se vatra e saj është .
Zgjidhje
Meqë vatra e saj është , nga kushti gjejmë parametrin:
Në këtë rast parabola do të ketë ekuacion .