Perpjesetimi. Vetite e perpjesetimit | Matematika 7

Perpjesetim quhet barazim i dy raporteve.

Numrat që formojnë perpjesetimin quhen kufiza të perpjesetimit. Këto mund të jenë numra të plotë, dhjetorë, thyesorë.

Këtë e shkruajmë dhe në mënyrën standarte $\displaystyle \frac{3}{2}=\frac{21}{14}$

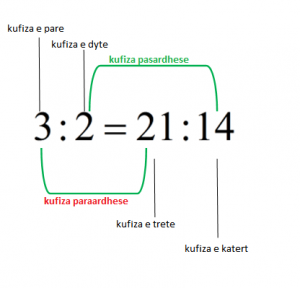
3 dhe 14 quhen kufiza të jashtme të perpjesetimit.

2 dhe 21 quhen kufiza të brëndshme të perpjesetimit.

Leximi i perpjesetimit bëhet: “Raporti i 3 me 2 është i barabartë me raportin e 21 me 14”.

Vetitë e perpjesetimit

Vetia themelore.“Në çdo përpjesetim, prodhimi i dy kufizave të jashtme është i barabartë me prodhimin e dy kufizave të brëndshme”.

$\displaystyle \frac{4}{7}=\frac{12}{21}$
sipas vetisë duhet: 4 ∙ 21 = 7 ∙ 12

Në formë të përgjithësuar shkruajmë:
$\displaystyle \frac{a}{b}=\frac{c}{d}<=>a\cdot d=b\cdot c$

Vetia e të anasjelltës.“Në çdo përpjesetim, po të zëvëndësojmë çdo raport të tij me të anasjelltën e tyre, formohet përpjesetim”.

$\displaystyle \frac{7}{6}=\frac{14}{12}<=>\frac{6}{7}=\frac{12}{14}$

Në formë të përgjithësuar shkruajmë:
$\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{b}{a}=\frac{d}{c}$

Vetia e ndërrimit.

“Në çdo përpjesetim, po t’u ndërrojmë vendet kufizave të jashtme me njëra-tjetrën formohet përpjesetim”.

$\displaystyle \frac{4}{9}=\frac{16}{36}<=>\frac{36}{9}=\frac{16}{4}$

Në formë të përgjithësuar shkruajmë:
$\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{d}{b}=\frac{c}{a}$

“Në çdo përpjesetim, po t’u ndërrojmë vendet kufizave të brëndshme me njëra-tjetrën formohet përpjesetim”.
$\displaystyle \frac{4}{9}=\frac{16}{36}<=>\frac{4}{16}=\frac{9}{36}$

Në formë të përgjithësuar shkruajmë:
$\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{a}{c}=\frac{b}{d}$

“Në çdo përpjesetim, po t’u ndërrojmë vendet ndërmjet tyre dy kufizave të brëndshme dhe dy kufizave të jashtme formohet përpjesetim”.
$\displaystyle \frac{4}{9}=\frac{16}{36}<=>\frac{36}{16}=\frac{9}{4}$

Në formë të përgjithësuar shkruajmë:
$\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{d}{c}=\frac{b}{a}$ .

Vetia në lidhje me mbledhjen ose ndryshesën e kufizave të çdo raporti të perpjesetimit.“Raporti i shumës (ndryshesës) ndërmjet kufizës së parë dhe të dytë përmbi kufizën e parë ose të dyte është e barabartë me shumën (ndryshesën) e kufizës së trëtë me të katërt përmbi kufizën e tretë ose të katërt”.

Për shumën kemi:

– $\displaystyle \frac{9}{4}=\frac{36}{16}<=>\frac{9+4}{4}=\frac{36+16}{16}$
– $\displaystyle \frac{9}{4}=\frac{36}{16}<=>\frac{9+4}{9}=\frac{36+16}{36}$

Në formë të përgjithësuar shkruajmë:
– $\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{a+b}{b}=\frac{c+d}{d}$
– $\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{a+b}{a}=\frac{c+d}{c}$

Për ndryshesën kemi:

– $\displaystyle \frac{9}{4}=\frac{36}{16}<=>\frac{9-4}{4}=\frac{36-16}{16}$
– $\displaystyle \frac{9}{4}=\frac{36}{16}<=>\frac{9-4}{9}=\frac{36-16}{36}$

Në formë të përgjithësuar shkruajmë:
– $\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{a-b}{b}=\frac{c-d}{d}$
– $\displaystyle \frac{a}{b}=\frac{c}{d}<=>\frac{a-b}{a}=\frac{c-d}{c}$

Vetia e kufizave paraardhëse dhe pasardhëse: “Në çdo perpjesetim, shuma (diferenca) e kufizave paraardhëse rri tek shuma (ndryshesa) e kufizave pasardhëse , sikundër rri çdo kufizë paraardhëse tek pasardhësja e saj“.

$\displaystyle \frac{9}{4}=\frac{36}{16}=\frac{9+36}{4+20}=\frac{45}{24}$
$\displaystyle \frac{36}{16}=\frac{9}{4}=\frac{36-9}{16-4}=\frac{27}{12}$

Në formë të përgjithësuar shkruajmë:
$\displaystyle \frac{a}{b}=\frac{c}{d}=\frac{a-c}{b-d}=\frac{a+c}{b+d}$

Njehsimi i kufizës së panjohur në një perpjesetim

Më poshtë japim rregullat e njehsimit të kufizës së panjohur në një perpjesetim:

Rregulli 1:

“Në një perpjesetim, vlera e një kufize të panjohur të jashtme është e barabartë me prodhimin e dy kufizave të brëndshme dhe ky prodhim i pjestuar me kufizën tjetër të jashtme ”.

$\displaystyle \frac{8}{6}=\frac{32}{x}$

$\displaystyle x=\frac{6\cdot 32}{8}$

$\displaystyle x=24$

Rregulli 2:

“Në një perpjesetim, vlera e një kufize të panjohur të brëndshme është e barabartë me prodhimin e dy kufizave tëjashtme dhe ky prodhim i pjestuar me kufizën tjetër të brëndshme ”.

$\displaystyle \frac{8}{x}=\frac{32}{24}$

$\displaystyle x=\frac{8\cdot 24}{32}$

$\displaystyle x=6$

Ushtrimet per kete mesim mund ti gjeni ketu