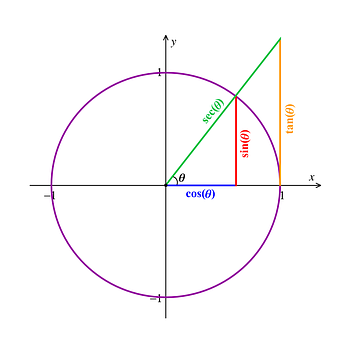
Trigonometri | Perkufizimet e funksioneve trigonometrike

Në mjaft probleme të jetës praktike lind nevoja për të njohur varësitë që ekzistojnë ndërmjet brinjëve dhe këndeve të trekëndëshit. Këto varësi i studion një degë e veçantë e quajtur trigonometria.

Trigonometria është bashkim i fjalëve trigon-trekëndësh dhe metri-matje.

Përkufizim: “Këndi qendror, i cili gjatësinë e harkut përkatës e ka të barabartë me rrezen e rrethit, quhet kënd 1 radian”.

Nuk duhet ngatërruar masa e harkut me gjatësinë e tij.

Pra, masa në radian gjendet:

$\displaystyle r=\frac{\pi n}{180}$ , ku r është masa në radian dhe n është masa në gradë.

Ndërtojmë masat në radian të këndeve kryesorë:

Masa në gradë	360º	180º	90º	60º	45º	30º
Masa në radian	2 π	π	$\displaystyle \frac{\pi }{2}$	$\displaystyle \frac{\pi }{3}$	$\displaystyle \frac{\pi }{4}$	$\displaystyle \frac{\pi }{6}$

Përkufizimet e funksioneve trigonometrike

Jepet trekëndëshi kënddrejtë me katete a dhe b, hipotenuzë c dhe këndin e ngushtë α.

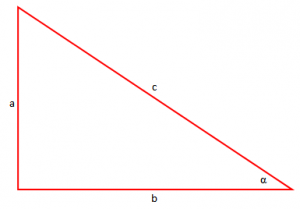
Përkufizim 1: “Sinus i këndi α (shënohet $\displaystyle \sin \alpha$ ) quhet raporti i katetit përballë këndit α me hipotenuzën”.

Pra, $\displaystyle \sin \alpha =\frac{a}{c}$ .

Përkufizim 2: “Kosinus i këndit α (shënohet $\displaystyle \cos \alpha$ ) quhet raporti i katetit të anëshkruar këndit α me hipotenuzën”.

Pra, $\displaystyle \cos \alpha =\frac{b}{c}$

Përkufizim 3: “Tangent i këndit α (shënohet $\displaystyle tg \alpha$ ) quhet raporti i katetit përballë këndit α me katetin anëshruar këndit α”.

Pra, $\displaystyle tg \alpha =\frac{a}{b}$

Përkufizim 4: “Kotangent i këndit α (shënohet $\displaystyle cot \alpha$ ) quhet raporti i katetit anëshruar këndit α me katetin përballë këndit α”.

Pra, $\displaystyle cot\alpha =\frac{b}{a}$ .

Është e qartë që vlerat e $\displaystyle \sin\alpha$ , $\displaystyle \cos\alpha$ , $\displaystyle tg\alpha$ dhe $\displaystyle cot\alpha$ varen vetëm nga madhësia e këndit α.

Disa përfundime:

Duke qënë raporte brinjësh, funksionet trigonometrike të këndeve janë numra pozitivë dhe abstraktë (nuk kanë njësi)
Duke qënë se gjatësitë e kateteve të trekëndëshit jnaë më të vogla se gjatësia e hipotenuzës, rrjedh se vlerat e funskioneve trigonometrike sinus dhe kosinus janë numra më të vegjël se 1. Pra, $\displaystyle 0\le \sin \alpha <1$ dhe $\displaystyle 0\le \cos \alpha <1$

Trigonometria është bashkim i fjalëve trigon-trekëndësh dhe metri-matje.

Përkufizimet e funksioneve trigonometrike

Postime te ngjashme: