Katerkendeshat | Llojet e katerkendeshave | Matematika 9

Katerkendeshat janë shumëkëndëshat që kanë katër brinjë.

Tek katerkendeshat, dy kulme jo fqinjë quhen kulme të kundërt të tij.

Dy brinjë jo fqinje tek katerkendeshat quhen brinjë të kundërta të tij.

Teoremë: “Shuma e këndeve të katërkëndëshit të mysët është 360º”.

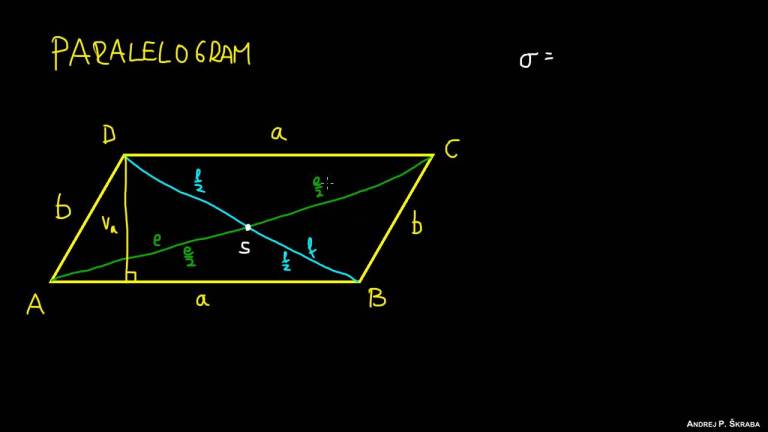
Paralelogrami

Përkufizim: “Paralelogram quhet katërkëndëshi që i ka brinjët dy nga dy paralele”.

Vetitë e paralelogramit

Vetia 1: “Në çdo paralelogram, brinjët paralele janë kongruente”.

Vetia 2: “Në çdo paralelogram, këndet e kundërt janë kongruentë”.

Vetia 3: “Diagonalet e paralelogramit përgjysmojnë njëra tjetrën ”.

Vetia 4: “Në çdo paralelogram, çdo dy kënde të njëpasnjëshëm e kanë shumën 180º”.

Vetia 5: “Çdo diagonale e ndanë paralelogramin në dy trekëndësha kongruentë”.

Vetia 6: “Diagonalet e ndajnë paralelogramin në katër trekëndësha, dy nga dy kongruentë”.

Kushtet kur një katërkëndësh është një paralelogram

Kur katërkëndëshi i ka brinjët e kundërta kongruente, ai është paralelogram
ose:
Kur një katërkëndësh i ka këndet e kundërta kongruente, ai është paralelogram.
ose:
Kur në një katërkëndësh, diagonalet përgjysmojnë njëra-tjetrën, ai është paralelogram.
ose:
Kur në një katërkëndësh, dy nga brinjët e kundërta janë kongruente dhe paralele, ai është paralelogram.

Rombi

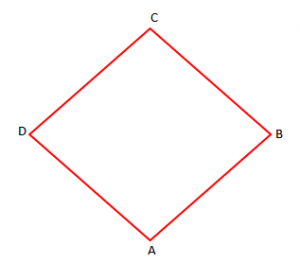
Përkufizim: “Romb quhet paralelogrami që ka dy brinjë fqinjë kongruente”.

AB = BC = CD = DA

Rombi është paralelogram dhe zotëron gjithe vetitë e tij që përmendëm më lart, por ka dhe këto veti të tjera:

Vetia 1: “Diagonalet e rombit janë pingule ndërmjet tyre”.

Vetia 2: “Rombi i ka diagonalet përgjysmore të këndeve të tij”.

Vetia 3: “Diagonalet e rombit, e ndajnë rombin në katër trekëndësha kongruentë”.

Kushtet që një paralelogram të jetë romb

Kur diagonalet e tij janë pingule.
Kur njëra nga diagonalet e tij të përgjysmoj njërin kënd.

Drejtkendeshi

Përkufizim: “Drejtekendesh quhet paralelogrami që ka një kënd të drejtë”.

$\displaystyle \angle A=\angle B=\angle C=\angle D=90{}^\text{o}$

Vetitë e drejtkendeshit

Vetia 1: “Drejtkëndëshi është paralelogram, pra gëzon gjithë vetitë e paralelogramit”.

Vetia 2: “Diagonalet e drejtkëndëshit janë kongruente”.

Kushti që një katërkëndësh të jetë drejtkëndësh

Kur diagonalet e tij janë kongruente dhe përgjysmojnë njëra-tjetrën.

Katrori

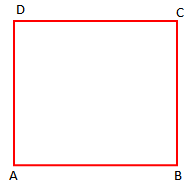
Përkufizim: “Katror quhet drejtkëndëshi që ka dy brinjë fqinjë kongruente”.

AB = BC = CD = DA

$\displaystyle \angle A=\angle B=\angle C=\angle D$

Katrori është paralelogram, është drejtkëndësh dhe romb.

Katrori i ka të gjitha vetitë e figurave që përmendëm më lart.

Gjithashtu, katrori ka dhe këto veti: Diagonalet e katrorit janë kongruente, pingule dhe përgjysmore të këndeve të tij.

Kushti që një paralelogram të jetë katror

Kur diagonalet janë kongruente dhe dhe pingule.
Kur diagonalet janë kongruente dhe njëra diagonale përgjysmon njërin kënd të tij.

Trapezi

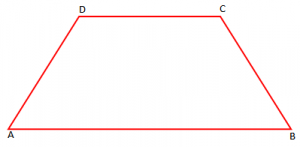
Përkufizim: “Trapez quhet katërkëndëshi tek i cili vetëm dy brinjë të kundërta janë paralele”.

$\displaystyle AB//CD$

Teoremë: “Vija e mesme e trapezit është paralele me bazat e tij dhe është sa gjysmë-shuma e tyre”.

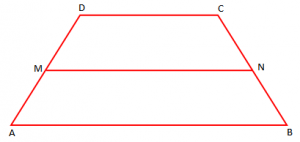
MN vijë e mesme e trapezit ABCD

$\displaystyle MN//AB//CD$

$\displaystyle MN=\frac{1}{2}\left( AB+CD \right)$

Teorema e Talesit

Tales i Miletit ka qënë një dijetar i shquar i antikitetit grek (shek VI p.e.s)

Teorema e Talesit thotë: “Nëse dy drejtëza paralele presin drejtëzat d dhe $\displaystyle {{d}_{1}}$ dhe caktojnë në d segmente kongruentë, atëherë ato caktojnë edhe në $\displaystyle {{d}_{1}}$ segmente kongruentë”.

Vija e mesme e trekëndëshit

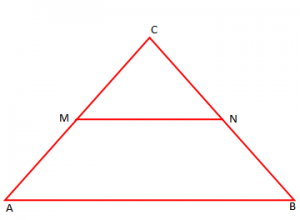
Teoremë: “Segmenti që bashkon meset e dy brinjëve të një trekëndëshi është paralel me brinjën e tretë dhe është sa gjysma e saj”.

MN – vijë e mesme e trekëndëshit

$\displaystyle MN//AB$

$\displaystyle MN=\frac{1}{2}AB$