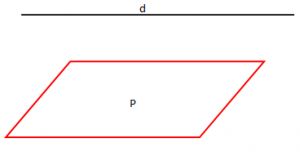
Plani është një sipërfaqe e sheshtë dhe e pakufizuar. Gjeometrikisht, plani paraqitet me anën e një paralelogrami, i cili përfytyrohet i shtrirë pa kufi.
Plani shënohet me një shkronjë të madhe të alfabetit, për shembull P, Q etj.
Kemi disa raste me drejtëzën dhe planin:
1. Drejtëza paralele me planin
Drejtëza d është paralele me planin P. Shkruajmë , ose
.
2. Drejtëza pingule me planin
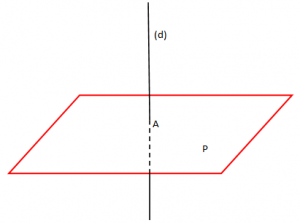
Drejtëza d është pingule me planin P. Shkruajmë
3. Drejtëza shtrihet në plan
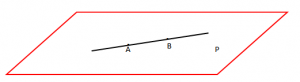
Në këtë rast vëmë re së të gjitha pikat e drejtëzës shtrihen në plan.
Shkruajmë
Gjendja e ndërsjelltë e dy drejtëzave dhe dy planeve në hapësirë
Ushtrimi 1
Kemi kuboidin ABCDMNPQ.
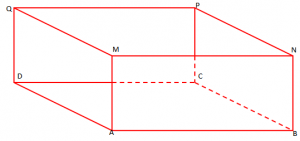
a) Sa pika të përbashkëta kanë drejtëzat BN dhe MN? Drejtëzat AD dhe AM? Drejtëzat AD dhe DC? Drejtëzat AD dhe DQ?
Përgjigje: Drejtëzat e mësipërme kanë vetëm një pikë të përbashkët. Ato janë drejtëza prerëse.
b) Sa pika të përbashkëta kanë drejtëzat AB dhe DC? Drejtëzat AB dhe MN? Drejtëzat BC dhe AD?
Përgjigje: Drejtëzat e mesipërme nuk kanë asnjë pikë të përbashkët. Ato janë drejtëza paralele.
c) Sa pika të përbashkëta kanë drejtëzat AB dhe DQ? Drejtëzat AD dhe BN?
Përgjigje: Drejtëzat e mësipërme nuk kanë asnjë pikë të përbashkët, por nuk janë drejtëza paralele sepse ato nuk ndodhen në të njëjtin plan. Ato ndodhen në plane të ndryshme. E para ndodhet në planin ABCD dhe e dyta ndodhet në planin MNPQ. Këto drejtëza quhen të kithëta.
Përkufizim: “Dy drejtëza quhen të kithëta nëse nuk ndodhen në një plan”.
Vëzhgojmë planet ABCD dhe MNPQ. Ato nuk kanë asnjë pikë të përbashkët.
Përkufizim: “Dy plane që nuk kanë asnjë pikë të përbashkët janë paralele”.
Shënojmë planin ABCD me P dhe planin MNPQ me Q dhe do të shkruajmë:
ose
.
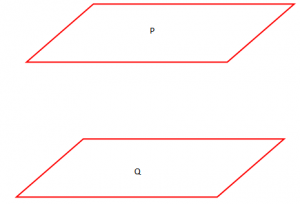
Ky është ilustrimi i planeve paralele.
Tek kuboidi ABCDMNPQ shohim faqet ABCD dhe ADMQ

Ato kanë brinjën AD të përbashkët.
Dy plane që nuk janë paralel kanë gjithmonë një drejtëz të përbashkët. Ato priten sipas një drejtëze.
Shkruajmë