Funksionet trigonometrike | Matematika 10

Funksionet trigonometrike i kemi trajtuar dhe në klasën e nëntë.

Në këtë artikull do të trajtojmë funksionet trigonometrike për kujtesën tuaj. Do të mësojmë si të konvertojmë gradët në radian dhe anasjelltas, si dhe përkufizimet për funksionet trifonometrike në gjysmërrethin trigonometrik.

Radiani

Një njësi tjetër për të matur harqe dhe kënde është radiani.

Fjala radian vjen nga fjala radio që do të thotë rreze.

Harku “1 radian” është harku “1 rreze”, që do të thotë “harku me gjatësi sa rrezja e rrethit”.

Vet rrethi ka 2π radian.

Shënojmë me A masën në gradë të një këndi ose harku dhe me B masën e tij në radian.

Është i vërtetë barazimi:

$\displaystyle \frac{A}{180{}^\text{o}}=\frac{B}{\pi }$ .

Për të kthyer nga radian në gradë mbani mend se $\displaystyle \pi =180{}^\text{o}$ .

Për shëmbull $\displaystyle 60{}^\text{o}$ është $\displaystyle \frac{180{}^\text{o}}{3}$ , pra $\displaystyle \frac{\pi }{3}$ .

Harku 1 radian është afërsisht $\displaystyle 57{}^\text{o}$ .

Shembull 1

Gjeni masën në gradë të këndeve:

a) $\displaystyle \frac{\pi }{2}$

b) $\displaystyle 2\pi$

c) $\displaystyle \frac{\pi }{4}$

d) $\displaystyle \frac{2\pi }{3}$

e) $\displaystyle \frac{5\pi }{6}$

Zgjidhje (a, b, c)

Për zgjidhjen e këtyre ushtrimeve zbatojmë formulën $\displaystyle \frac{A}{{{180}^{\text{o}}}}=\frac{B}{\pi }$

a) $\displaystyle \frac{\pi }{2}$

Në këtë rast $\displaystyle B=\frac{\pi }{2}$ . Do të kemi:

$\displaystyle \frac{A}{{{180}^{\text{o}}}}=\frac{\frac{\pi }{2}}{\pi }$

$\displaystyle \frac{A}{{{180}^{\text{o}}}}=\frac{1}{2}$

$\displaystyle A=\frac{180{}^\text{o}}{2}=90{}^\text{o}$

b) $\displaystyle 2\pi$

Në këtë rast $\displaystyle B=2\pi$ . Do të kemi:

$\displaystyle \frac{A}{{{180}^{\text{o}}}}=\frac{2\pi }{\pi }$

$\displaystyle \frac{A}{{{180}^{\text{o}}}}=2$

$\displaystyle A={{180}^{\text{o}}}\cdot 2={{360}^{\text{o}}}$

c) $\displaystyle \frac{\pi }{4}$

Në këtë rast $\displaystyle B=\frac{\pi }{4}$ . Do të kemi:

$\displaystyle \frac{A}{{{180}^{\text{o}}}}=\frac{\frac{\pi }{4}}{\pi }$

$\displaystyle \frac{A}{{{180}^{\text{o}}}}=\frac{1}{4}$

$\displaystyle A=\frac{{{180}^{\text{o}}}}{4}=90{}^\text{o}$

Shembull 2

Gjeni masën në gradë radian të këndeve:

a) 1º

b) 30º

c) 45º

d) 60º

e) 90º

f) 180º

g) 270º

h) 300º

i) 360º

Zgjidhje (a, b, c)

Për zgjidhjen e këtyre ushtrimeve zbatojmë formulën $\displaystyle \frac{A}{{{180}^{\text{o}}}}=\frac{B}{\pi }$

a) A=1º

$\displaystyle \frac{1{}^\text{o}}{{{180}^{\text{o}}}}=\frac{B}{\pi }$

$\displaystyle B=\frac{\pi }{180}$

b) A=30º

$\displaystyle \frac{30{}^\text{o}}{{{180}^{\text{o}}}}=\frac{B}{\pi }$

$\displaystyle B=\frac{30\pi }{180}=\frac{\pi }{6}$

c) A=45º

$\displaystyle \frac{45{}^\text{o}}{{{180}^{\text{o}}}}=\frac{B}{\pi }$

$\displaystyle B=\frac{45\pi }{180}=\frac{\pi }{4}$

Përkufizimi i funksioneve trigonometrike

Ne kemi shqyrtuar funksionet trigonometrike në gjysmërrethin trigonometrik. Shënojmë me x masën në radian ose në gradë të një harku AM ose këndin AOM në gjysmërrethin trigonometrik.

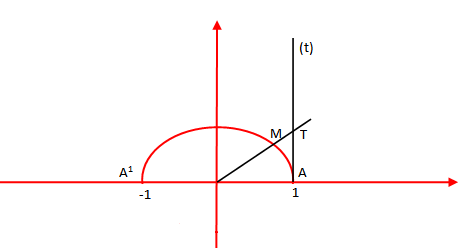
Përkufizime:

Sinus i x-it quhet ordinata e pikës M. Pra, $\displaystyle \sin x={{y}_{M}}$

Kosinus i x-it quhet abshisa e pikës M. , $\displaystyle \cos x={{x}_{M}}$

Tangjent i x-it quhet raporti i sinx me cosx. Pra, $\displaystyle \tan x=\frac{\sin x}{\cos x}$

Kotangjent i x-it quhet raporti i cosx me sinx. Pra, $\displaystyle \cot x=\frac{\cos x}{\sin x}$ .

Dy kënde me shumë 90º

Ne kemi mësuar se:

$\displaystyle \sin (90{}^\text{o}-x)=\cos x$
$\displaystyle \cos (90{}^\text{o}-x)=\sin x$
$\displaystyle \tan(90{}^\text{o}-x)=\cot x$
$\displaystyle \cot(90{}^\text{o}-x)=\tan x$