Home / Vellimi i trupave. Parimi i kavalierit

Vellimi i trupave. Parimi i kavalierit

vellimi i trupave. Parimi i kavalierit

Pjesa e hapësirës që zë një trup quhet vëllim i këtij trupi.

Të gjesh vëllimin e një trupi do të thotë ta krahasosh atë me një trup tjetër, i cili merret si njësi, pra ta caktosh sa herë vëllimi i trupit përmban vëllimin njësi.

Si njësi e vëllimit merret vëllimi i kubit me brinjë një njësi të gjatësisë. Kjo njësi quhet njësi kubike, për shembull \displaystyle 1~c{{m}^{3}}, \displaystyle 1~{{m}^{3}} etj.

 

 

 

 

Vëllimi i kuboidit

Kemi parë se vëllimi i kuboidit me përmasa a,b,c është i barabartë me prodhimin e tyre, pra V = a∙b∙c

Nëse shënojmë me S sipërfaqen e bazës së kuboidit dhe me h lartësinë e tij, formula e mësipërme merr trajtën V = S∙h

Rrjedhim: Vëllimi i kubit me brinjë a jepet me formulën \displaystyle V={{a}^{3}}.

 

 

 

 

 

Parimi i kavalierit

Parimi i kavalierit është formuluar nga matematikani Kavalier në vitin 1635.

Parimi i kavalierit: Në qoftë se dy trupa janë vendosur në një plan α, në mënyrë që prerjet përkatëse të tyre me çdo paralel me këtë plan të kenë sipërfaqe të barabarta, atëherë këta trupa kanë vëllime të barabarta.

 

 

 

 

Vellimi i prizmit

Vellimi i prizmit është i barabartë me prodhimin e sipërfaqes së bazës me lartësinë e tij.

Gjithmonë tek prizmi i drejtë, lartësia është brinja e tij.

\displaystyle V={{S}_{b}}\cdot l

 

 

 

Ushtrim

Jepet prizmi me bazë trapez dhe lartësi 12 cm.
Baza e madhe e trapezit është 8 cm, baza e vogël është 4 cm, lartësia e trapezit është 6 cm dhe brinjët anësore jane nga 6 cm.

Gjeni:

a) Sipërfaqen anësore të prizmit

b) Sipërfaqen e bazës së prizmit

c) Sipërfaqen e përgjithshme të prizmit

d) Vëllimin e prizmit

 

Zgjidhje

 

Ndërtojmë në fillim prizmin me bazë trapez

 

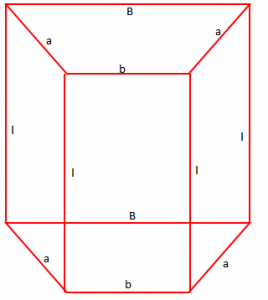
prizmi

Kemi të dhënë:

l = 12 cm

B = 8 cm

b = 4 cm

h = 6 cm

 

 

a) Gjejmë sipërfaqen anësore

Nga formula dimë që:

\displaystyle {{S}_{a}}=p\cdot l

 

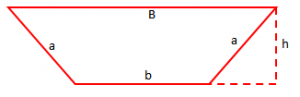
trapezi

Gjejmë perimetrin e bazës, pra perimetrin e trapezit

P = 2a + b + B

P = 2 ∙ 6 + 4 + 8

P = 12 + 12

P = 24 cm

 

Tani gjejmë sipërfaqen anësore të prizmit me bazë trapez:

\displaystyle {{S}_{a}}=p\cdot l

\displaystyle {{S}_{a}}=24\cdot 12

\displaystyle {{S}_{a}}=288c{{m}^{2}}

 

 

b) Gjejmë sipërfaqen e bazës

Në fillim gjejmë sipërfaqen e trapezit:

 

trapezi

\displaystyle {{S}_{T}}=\frac{\left( B+b \right)\cdot h}{2}

\displaystyle {{S}_{T}}=\frac{\left( 8+4 \right)\cdot 6}{2}

\displaystyle {{S}_{T}}=12\cdot 3

\displaystyle {{S}_{T}}=36c{{m}^{2}}

 

Tani për të gjetur sipërfaqen e bazës e shumëzojmë këtë sipërfaqe me 2:

\displaystyle {{S}_{b}}=2\cdot 36

\displaystyle {{S}_{b}}=72c{{m}^{2}}

 

 

c) Gjejmë sipërfaqen e përgjithshme

Nga formula, dimë që:

\displaystyle {{S}_{p}}={{S}_{a}}+{{S}_{b}}

Pra, do të kemi:

\displaystyle {{S}_{p}}=288+72

\displaystyle {{S}_{p}}=360c{{m}^{2}}

 

 

d) Gjejmë vëllimin e prizmit

Nga formula dimë që:

\displaystyle {{V}_{p}}={{S}_{b}}\cdot l (sipërfaqen e njërës bazë).

Pra, do të kemi prodhimin e sipërfaqes së trapezit me lartësinë e prizmit:

\displaystyle {{V}_{p}}=36\cdot 12

\displaystyle {{V}_{p}}=432c{{m}^{3}}

 

 

Në rastin kur prizmi është kuboid, vellimi gjendet duke shumëzuar tri përmasat e kuboidit. Pra, \displaystyle V=a\cdot b\cdot c.

Për kubin kemi a = b = c dhe \displaystyle V={{a}^{3}}.

 

Shembull

Gjeni vëllimin e kuboidit me përmasa 3, 4 dhe 5 cm.

 

Zgjidhje

 

Nga formula, dimë që vellimi i kuboidit gjendet duke shumëzuar tri përmasat e tij. Pra, do të kemi:

\displaystyle V=3\cdot 4\cdot 5=60c{{m}^{3}}.

Copyright © detyra.al
Postime te ngjashme: