Vazhdueshmeria e funksionit | Matematika 12

Përkufizim: Funksioni f quhet i vazhdueshëm në pikën a , në qoftë se ekziston limiti i tij kur është i barabartë me f(a).

Pra f i vazhdueshëm në pikën a => ekziston $\underset{x\to a}{\mathop{\lim }}\,f(x)=f(a)$

Themi se funksioni është i vazhdueshëm ne pikën a duhet që të plotësojë njëherësh 3 kushtet

Funksioni f të jetë i përcaktuar në pikën a.
Të ekzistojë $\underset{x\to a}{\mathop{\lim }}\,f(x)$
$\underset{x\to a}{\mathop{\lim }}\,f(x)=f(a)$ (pra të jetë e barabartë sa vlera e funksionit në pikën x=a).

Pika në të cilen funksioni nuk është i vazhdueshëm quhet pikë këputje e funksionit.

Përdoret ky emërtim, sepse në këtë pikë grafiku i funksionit ka këputje.

Veprimet me funksionet e vazhdueshem

Për tu njohur me veprimet e funksionit të vazhdueshëm ne bazohemi në 4 teoremat e saj:

Teorema 1: Në qoftë se funksionet f,g janë të vazhdueshme në pikën a, atëherë dhe funksioni s=f+g është i vazhdueshëm në pikën a.

Teorema 2: Nëse funksionet f,g janë të vazhdueshme në pikën a, atëherë dhe funksioni p=f∙g është i vazhdueshëm në pikën a.

Teorema 3: Nëse funksionet f,g janë të vazhdueshme në pikën a dhe g(a)≠0, atëherë edhe funksioni $h=\frac{f}{g}$ është i vazhdueshëm në pikën a.

Teorema 4: Në qoftë se funksioni φ:u= φ(x) është i vazhdueshëm në pikën a dhe funksioni f:y=f(u) është i vazhdueshëm në pikën ${{u}_{1}}=\varphi (a)$ , atëherë edhe funksioni i përbërë ${{f}_{o\varphi }}$ është i vazhdueshëm në pikën a.

Vazhdueshmëria e funksioneve të zakonshme

Në klasën e 11-të kemi parë që funksionet e mëposhtëme, në çdo pikë të bashkësisë së tyre të përcaktimit kanë limit, të barabartë me vlerën e tyre në këtë pikë.

Funksioni konstant y=c, ku c- numër real.
Funksioni fuqi $\displaystyle y={{x}^{\alpha }}$ , ku α- numër real.
Funksionet eksponencial $\displaystyle y={{a}^{x}}$ , ku $\displaystyle 0<a\ne 1$ .
Funksioni logaritmik $\displaystyle y={{\log }_{a}}x$ , ku $\displaystyle 0<a\ne 1$ .
Funksionet trigonometrike $\displaystyle y=\sin x,~~y=\cos x,~~y=tgx$ .
Funksioni $\displaystyle y=|x|$ .

Pra, secili nga këto funksione është i vazhdueshëm në çdo pikë të bashkësisë së tij të përcaktimit.

Përkufizim: “Funksion i zakonshëm quhet çdo funksion numerik që mund të jepet me një formulë të vetme të trajtës $\displaystyle y=f\left( x \right)$ , të marrë duke kryer një numër të fundëm veprimesh aritmetike (mbledhje, zbritje, shumëzim, pjesëtim) dhe një numër të fundëm veprimesh të marrjes së përbërjes së funksioneve, prej funksioneve të mësipërme”.

Për shembull, funksioni $\displaystyle y=x+\sqrt{{{x}^{2}}+9}+\ln \left( \sin x+\cos x \right)$ është funksion i zakoshëm, kurse funksioni:

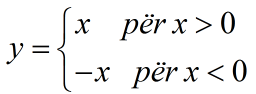
nuk është funksion i zakonshëm.

Ushtrimi 1

Gjeni bashkësinë ku është i vazhdueshëm funksioni $\displaystyle y=\sqrt{-{{x}^{2}}+2x+3}$

Zgjidhje

Bashkësia ku funksioni është i vazhdueshëm funksioni $\displaystyle y=\sqrt{-{{x}^{2}}+2x+3}$ është bashkësia e tij e përcaktimit, sepse funksioni është i vazhdueshëm.

Bashkësia e përcaktimit është $\displaystyle -{{x}^{2}}+2x+3\ge 0$ .