Limitet e njeanshme . Limitet | Matematika 12

Limitet e funksioneve i kemi trajtuar në klasën e 11-të.

Le të kemi një funksion të përcaktuar në $\displaystyle \left] a,b \right[$

Përkufizim 1: “Numri $l$ quhet limit i djathtë i funksionit f kur $x\to a$ , nëse $\displaystyle |f\left( x \right)-l|$ bëhet sat ë duam ne e vogël, me kusht që të shqyrtohen vlera të $\displaystyle x>a$ , mjaft afër a”.

Më saktë, numri $\displaystyle l$ quhet limit i djathtë i funksionit f kur $\displaystyle x\to a$ nëse sidoqoftë numri $\displaystyle \varepsilon >0$ , gjejmë një numër pozitiv r, të tillë që për $\displaystyle x\in \left] a,a+r \right[$ të kemi $\displaystyle |f\left( x \right)-l|<\varepsilon$ . Shënohet $\displaystyle \underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)=l$ . Le të kemi një funksion të përcaktuar në $\displaystyle \left] c,a \right[$ . Përkufizim 2: “Numri $\displaystyle l$ quhet limit i majtë i funksionit f kur $\displaystyle x\to a$ , nëse diferenca $\displaystyle |f\left( x \right)-l|$ bëhet sat ë duam ne e vogël, nëse zgjidhen vlera të x<a, mjaft afër a”.

Më saktë, numri $\displaystyle l$ quhet limit i majtë funksionit f kur $\displaystyle x\to a$ nëse sidoqoftë numri $\displaystyle \varepsilon >0$ , gjejmë një numër pozitiv r, të tillë që për $\displaystyle x\in \left] a-r,a \right[$ të kemi $\displaystyle |f\left( x \right)-l|<\varepsilon$ . Shënojmë $\displaystyle \underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)=l$ .

Ushtrimi 1

Gjeni limitet e njëanëshme të funksionit

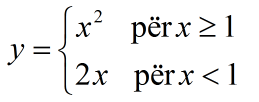
Zgjidhje

Gjejmë limitin e djathtë të funksionit kur $\displaystyle x\to 1$ :

$\displaystyle \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,{{x}^{2}}={{1}^{2}}=1$

Gjejmë limitin e majtë të funksionit kur $\displaystyle x\to 1$ :

$\displaystyle \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,2x=2\cdot 1=2$ .

Në këtë rast kemi që limitet e njëanëshme kanë vlera të ndryshme.

Përkufizim 3: “Funksioni f ka limit $\displaystyle l$ kur $\displaystyle x\to a$ , atëherë dhe vetëm atëherë kur limitet e njëanëshme, kur $\displaystyle x\to a$ , ekzistojnë dhe janë të barabarta me l”.

Ushtrime te zgjidhura

Ushtrimi 1

Gjeni limitet e njëanëshme te funksioneve më poshtë.

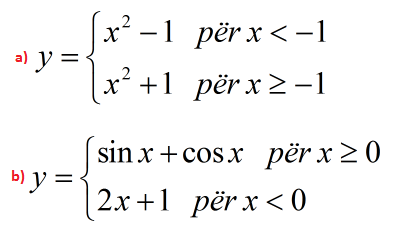
Zgjidhje

a) $\displaystyle \underset{x\to -{{1}^{-}}}{\mathop{\lim }}\,{{x}^{2}}-1={{\left( -1 \right)}^{2}}-1=0$

$\displaystyle \underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,{{x}^{2}}+1={{\left( -1 \right)}^{2}}+1=2$

b) $\displaystyle \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\sin x+\cos x=0+1=1$

$\displaystyle \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,2x+1=2\cdot 0+1=1$

Në këtë rast shkruajmë:

$\displaystyle \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,2x+1=\underset{x\to 0+}{\mathop{\lim }}\,\sin x+\cos x=1$

Ushtrimi 2

Gjeni vlerën e a që funksionet e mëposhtme të kenë limit kur $\displaystyle x\to 1$ .

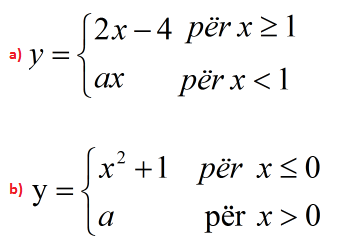
Zgjidhje

a) Meqë funksionet kanë limit kur $\displaystyle x\to 1$ , atëherë duhet të barazojmë limitet e njëanëshme dhe të gjejmë vlerën e a-së.

$\displaystyle \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,2x-4=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,ax~$ .

Gjejmë limitin e djathtë:

$\displaystyle \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,2x-4=2-4=-2$ .

Barazojmë limitin e majtë me vlerën që gjetëm:

$\displaystyle \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,ax~=-2\Rightarrow a=2$

b) Në të njëjtën mënyrë veprojmë dhe për këtë rast:

$\displaystyle \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,{{x}^{2}}+1=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,a~$

$\displaystyle \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,{{x}^{2}}+1=1+1=2$

$\displaystyle \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,a~=2\Rightarrow a=2$