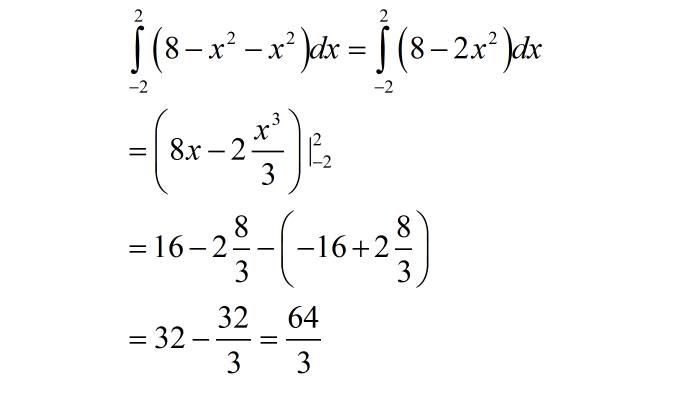
Ushtrime te zgjidhura – Integrali i caktuar
Ushtrimi 1
Të njehsohen integralet:
a)
b)
c)
Zgjidhje
a)
Zbatojmë vetitë e integralit të caktuar:
b)
c)
Nga tabela e integraleve themelore shkruajmë:
Ushtrimi 2
Të njehsohet integrali 
Zgjidhje
Ushtrimi 3
Të njehsohen integralet:
a)
b)
c)
Zgjidhje
a)
b)
c)
Ushtrimi 4
Të llogaritet sipërfaqja e figurës plane të kufizuar nga grafiku i funksionit , boshti i abshisave dhe drejtëzat
dhe
.
Zgjidhje
Për të gjetur sipërfaqen e figurës plane e kemi shume kollaj, sepse kemi funksionin si dhe kufijtë e integrimit. Shkruajmë:
Ushtrimi 5
Të llogaritet sipërfaqja e figurës së kufizuar nga drejtëzat ;
;
dhe
.
Zgjidhje
Kemi funksionin dhe kufijtë e integrimit të përcaktuar, ndaj shkruajmë:
Ushtrimi 6
Të llogaritet sipërfaqja e figurave plane të kufizuar nga vijat:
a) dhe
b) dhe
c) dhe
d) dhe
Zgjidhje
a) dhe
Gjejmë kufijtë e integrimit, duke gjetur pikën e përbashkët të dy funksioneve:
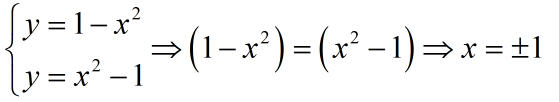
Ndërtojmë grafikët e funksioneve:
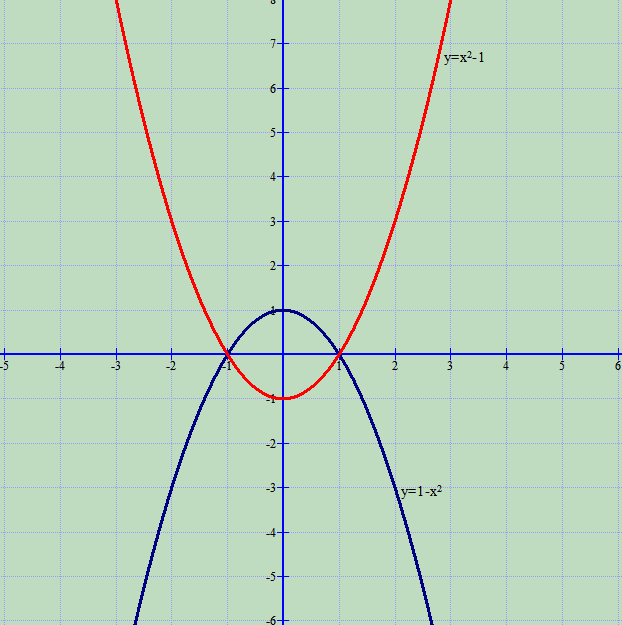
Siç shihet nga figura, për intervalin , kemi
, prandaj do të kemi:
b) dhe
Gjejmë kufijtë e integrimit, duke gjetur pikën e përbashkët të dy funksioneve:
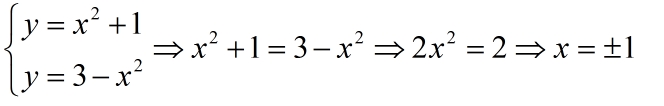
Ndërtojmë grafikët e funksioneve:
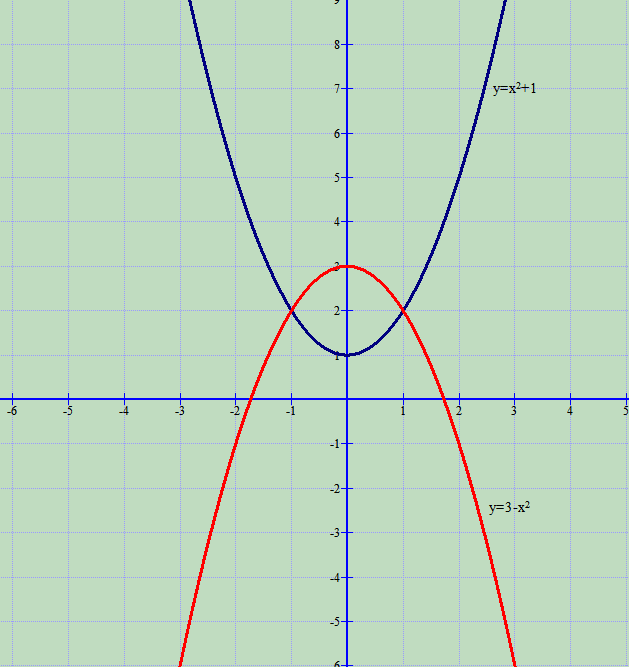
Siç shihet në figurë, në intervalin , kemi
, kështu formohet integrali:
c) dhe
Gjejmë kufijtë e integrimit, duke gjetur pikën e përbashkët të dy funksioneve:
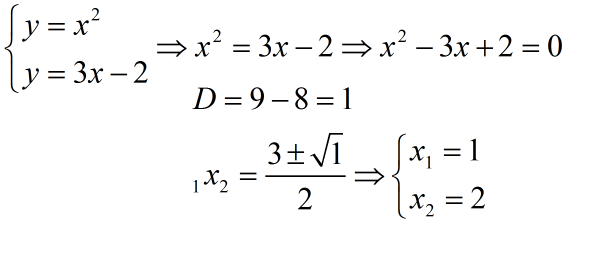
Ndërtojmë grafikët e funksioneve:
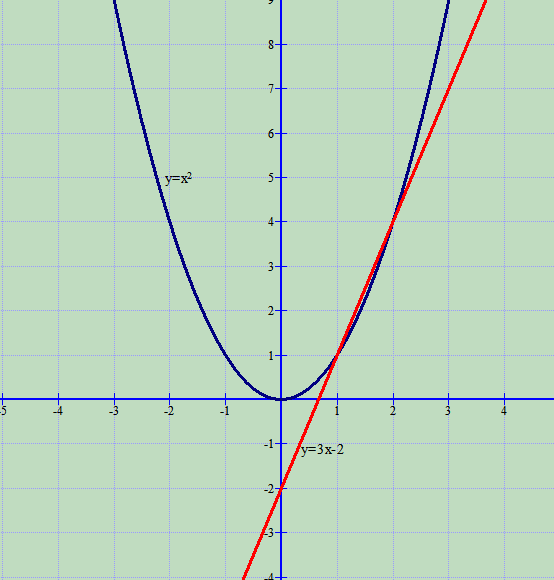
Siç shihet në figurë, në intervalin kemi
, kështu formohet integrali:
d) dhe
Gjejmë kufijtë e integrimit, duke gjetur pikën e përbashkët të dy funksioneve:
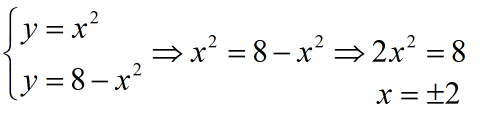
Ndërtojmë grafikët e funksioneve:
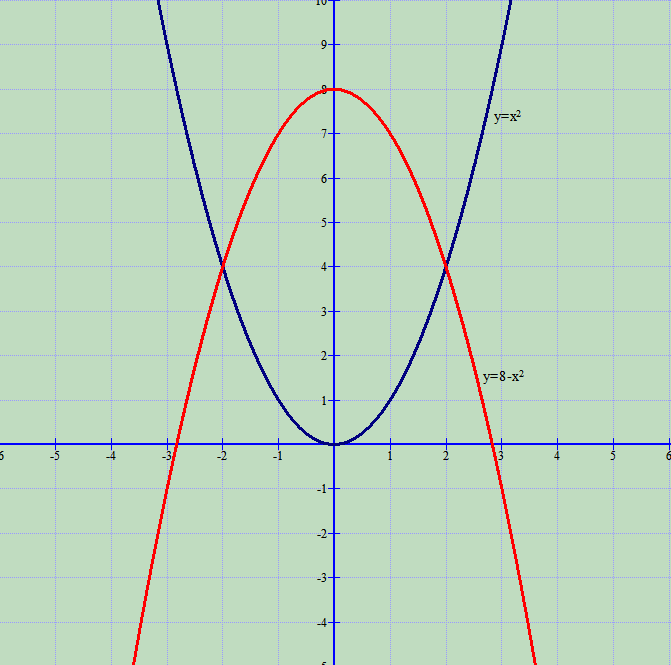
Siç shihet në figurë, në intervalin kemi
, kështu formohet integrali:

