Shumefaqeshat

Shumëfaqësh quhet trupi i kufizuar nga shumëkëndësha.

Shumëkëndëshat që kufizojnë shumëfaqëshin quhen faqe të shumëfaqëshit.

Në figurën më sipër, faqet janë ABCD, ABMN, AMQD, DCPQ, BCPN, MNPQ;

Brinjët e shumëkëndëshave quhen brinjë të shumëfaqëshit.

Për shembull AB; CD; MN etj.

Kulmet e shumëkëndëshave quhen kulme të shumëfaqëshit.
Për shembull A; B; C etj.

Prizmi

Përkufizim: “Prizëm n-këndor quhet shumëfaqëshi, dy faqe të të cilit janë n-këndësha që gjenden në plane paralele, kurse n-faqet e tjera janë paralelograme”.

Shumëkëndëshat paralelë quhen baza të prizmit, të cilat janë shumëkëndësha të barabartë.

Paralelogramet quhen faqe anësore të prizmit.

Brinjët AM, BN, CP dhe DQ të këtyre paralelogrameve quhen brinjë anësore të prizmit. Të gjitha brinjët anësore janë të barabarta.

Lartësi e prizmit quhet largesa ndërmjet planeve të bazave.

Bazat e prizmit mund të jenë trekëndësh, katërkëndësh, pesëkëndësh etj dhe quhen përktaësisht prizëm me bazë trekëndor, katërkëndor, pesëkëndor.

Prizmi quhet i drejtë, në qoftë se brinjët anësore të tij janë pingule me bazat.

Në një prizëm të drejt,brinjët anësore janë drejtkëndësha, ndërsa brinja anësore e tij shërben edhe si lartësi.

Prizmi i drejtë, i cili e ka bazën drejtkëndësh quhet kuboid. Të gjitha faqet e kuboidit janë drejtkëndësha.

Kuboidi që i ka të gjitha faqet katrorë quhet kub.

Teoremë: “Në qoftë se një prizëm e presim me një plan paralel me bazat e tij, atëherë prerja është shumëkëndësh i barabartë me shumëkëndëshat e bazave”.

Sipërfaqja e prizmit

• Sipërfaqja anësore

Sipërfaqja anësore është një drejtkëndësh që ka si gjatësi perimetrin e bazës dhe gjerësi lartësinë e prizmit.

P – Perimetri i shumëkëndëshit të bazës së prizmit

l – Lartësia e prizmit, në këtë rast brinjët AA₁, BB₁ dhe CC₁.

• Sipërfaqja e bazës

Sipërfaqja e bazës gjendet duke mbledhur 2 sipërfaqet e figurave të bazës tek prizmi.

Sipërfaqja e bazës tek prizmi gjendet në varësi të llojit të bazës që ka prizmi.

Në këtë rast e kemi trekëndësh dhe sipas formulës që kemi mësuar për trekëndëshin,nxjerrim që:

• b është baza e trekëndëshi, pra AB
• h është lartësia e ndërtuar mbi këtë trekëndësh.

• Sipërfaqja e përgjithshme

Sipërfaqja e përgjithshme, si çdo trup, edhe tek prizmi gjendet duke mbledhur sipërfaqen anësore me sipërfaqen e bazës. Pra, do të kemi:

Vëllimi i prizmit

Vëllimi i prizmit është i barabartë me prodhimin e sipërfaqes së bazës me lartësinë e tij.

Gjithmonë tek prizmi i drejtë, lartësia është brinja e tij.

Ushtrim

Jepet prizmi me bazë trapez dhe lartësi 12 cm.
Baza e madhe e trapezit është 8 cm, baza e vogël është 4 cm, lartësia e trapezit është 6 cm dhe brinjët anësore jane nga 6 cm.

Gjeni:

a) Sipërfaqen anësore të prizmit

b) Sipërfaqen e bazës së prizmit

c) Sipërfaqen e përgjithshme të prizmit

d) Vëllimin e prizmit

Zgjidhje

Ndërtojmë në fillim prizmin me bazë trapez

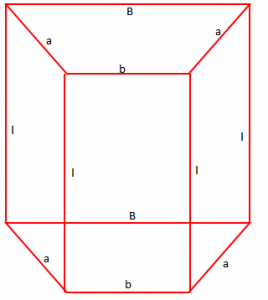
Kemi të dhënë:

l = 12 cm

B = 8 cm

b = 4 cm

h = 6 cm

a) Gjejmë sipërfaqen anësore

Nga formula dimë që:

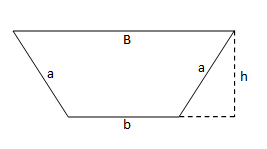
Gjejmë perimetrin e bazës, pra perimetrin e trapezit

P = 2a + b + B

P = 2 ∙ 6 + 4 + 8

P = 12 + 12

P = 24 cm

Tani gjejmë sipërfaqen anësore të prizmit me bazë trapez:

b) Gjejmë sipërfaqen e bazës

Në fillim gjejmë sipërfaqen e trapezit:

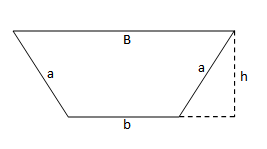
Tani për të gjetur sipërfaqen e bazës e shumëzojmë këtë sipërfaqe me 2:

c) Gjejmë sipërfaqen e përgjithshme

Nga formula, dimë që:

Pra, do të kemi:

d) Gjejmë vëllimin e prizmit

Nga formula dimë që:

(sipërfaqen e njërës bazë).

Pra, do të kemi prodhimin e sipërfaqes së trapezit me lartësinë: