Rrethi. Ekuacioni i rrethit | Matematika 12

Ekuacioni i rrethit

Përkufizim: Rreth quhet bashkësia e pikave të planit, të cilat kanë të njëjtën largesë mga një pikë fikse e planit.

Pika fikse quhet qendër e rrethit. Atë e shënojmë me O.

Largesa nga qëndra e tij quhet rreze e rrethit. Rrezen e rrethit e shënojmë me r.

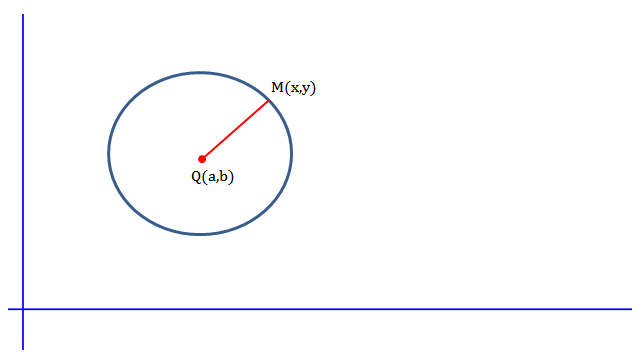
Në plan zgjedhim një sistem koordinativ xOy dhe shënojmë me a dhe b koordinatat e qendrës Q.

Në plan marrim një pikë çfarëdo $\displaystyle M\left( x,y \right)$ .

Nga përkufizimi, pika M është qendër e rrethit, atëherë dhe vetëm atëherë kur $\displaystyle QM=r$

Nga formula që jep largesën e dy pikave kemi:

$\displaystyle QM=\sqrt{{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}}$ .

Meqë $\displaystyle QM=r$ , kemi:

$\displaystyle r=\sqrt{{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}}$

$\displaystyle {{r}^{2}}={{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}$ .

Nga ky baraziim del se në qoftë se pika $\displaystyle M\left( x,y \right)$ është pikë e rrethit, koordinatat e saj vërtetojnë ekuacionin $\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ dhe anasjelltas, nëse koordinatat $\displaystyle \left( x,y \right)$ të pikës M vërtetojnë ekuacionin $\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ , atëherë kjo pikë ndodhet në rreth.

Në këtë mënyrë kemi provuar se ekuacioni i rrethit me qendër $\displaystyle Q(a,b)$ dhe rreze r është $\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ .

Ky ekuacion quhet ekuacioni më i thjeshtë i rrethit.

Ekuacionin $\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ mund ti japim një trajtë tjetër, duke zbërthyer katrorët:

$\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}-{{r}^{2}}=0$

$\displaystyle {{x}^{2}}-2ax+{{a}^{2}}+{{y}^{2}}-2by+{{b}^{2}}-{{r}^{2}}=0$

$\displaystyle {{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}+{{b}^{2}}-{{r}^{2}}=0$

Shënojmë $\displaystyle -2a=A$ ; $\displaystyle -2b=B$ ; $\displaystyle {{a}^{2}}+{{b}^{2}}-{{r}^{2}}=C$ dhe do të kemi:

$\displaystyle {{x}^{2}}+{{y}^{2}}+Ax+By+C=0$

Ky quhet ekuacioni i përgjithshëm i rrethit.

Vëmë re se ky ekuacion është ekuacion i fuqisë së dytë në lidhje me x, y me këto cilësi:

Koeficientët e kufizave $\displaystyle {{x}^{2}}$ dhe $\displaystyle {{y}^{2}}$ janë të barabartë.
Mungon kufiza e prodhimit $\displaystyle x\cdot y$ .