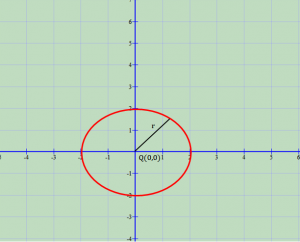
Raste te vecanta te ekuacionit te rrethit

Raste te veçanta te ekuacionit te rrethit

Kemi disa raste të veçanta te ekuacionit të rrethit. Do ti shikojmë ato me radhë:

Rrethi me qender në origjinën e koordinatave

Në këtë rast kemi $\displaystyle a=b=0$ .

Ekuacioni i rrethi do të ketë trajtën $\displaystyle {{x}^{2}}+{{y}^{2}}={{r}^{2}}$ .

Rrethi tangjent me boshtin e abshisave

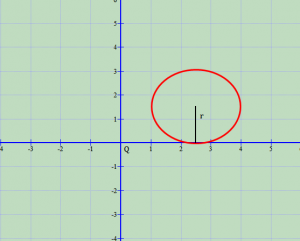
Në këtë rast do të kemi $\displaystyle b=r$ .

Ekuacioni i rrethit do të jetë $\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}$ .

Rrethi tangjent me boshtin e ordinatave

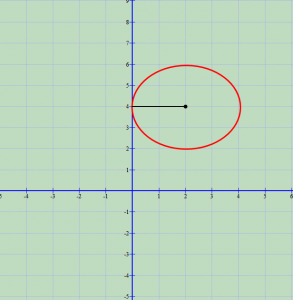
Në këtë rast do të kishim $\displaystyle a=r$ .

Ekuacioni i rrethit do të jetë $\displaystyle {{\left( x-r \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ .

Rrethi tangjent me boshtet koordinative

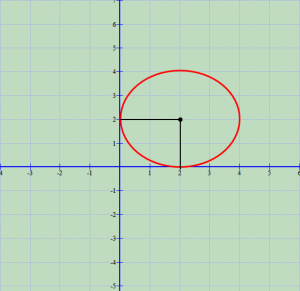
Në këtë rast do të kishim $\displaystyle a=b=r$ . Ekuacioni i rrethit do të ishte $\displaystyle {{\left( x-r \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}$ .

Ushtrime të zgjidhura – Raste të veçanta të ekuacionit të rrethit

Ushtrimi 1

Të shkruhet ekuacioni i rrethit me qendër $\displaystyle Q\left( -2,3 \right)$ v, në qoftë se pika $\displaystyle M\left( 0,1 \right)$ ndodhet në të.

Zgjidhje

Dimë që ekuacioni i rrethit është $\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ .

Zëvëndësojmë vlerat e x, y për të gjetur rrezen e rrethit:

$\displaystyle {{\left( 0+2 \right)}^{2}}+{{\left( 1-3 \right)}^{2}}={{r}^{2}}$

$\displaystyle {{r}^{2}}=4+4=8$ .

Ta shkruajmë ekuacionin e rrethit:

$\displaystyle {{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=8$ .

Ushtrimi 2

Të shkruhet ekuacioni i rrethit tangjet me boshtin e abshisve në pikën $\displaystyle M\left( 4,0 \right)$ (në boshtin e parë) dhe $\displaystyle r=2$ .

Zgjidhje

Në këtë rast kemi $\displaystyle b=r$ , pra do të shkruajmë:

$\displaystyle {{\left( x-4 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{2}^{2}}$

$\displaystyle {{\left( x-4 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4$

Ushtrimi 3

Të shkruhet ekuacioni i rrethit tangjent me boshtin e ordinatave, në pikën $\displaystyle M\left( 0,5 \right)$ (në boshtin e parë) dhe $\displaystyle r=3$ .

Zgjidhje

Në këtë rast kemi $\displaystyle a=r$ , pra do të shkruajmë:

$\displaystyle {{\left( x-3 \right)}^{2}}+{{\left( y-5 \right)}^{2}}={{3}^{2}}$

$\displaystyle {{\left( x-3 \right)}^{2}}+{{\left( y-5 \right)}^{2}}=9$ .

Ushtrimi 4

Jepen rrathët $\displaystyle {{x}^{2}}-2x+{{y}^{2}}+8y-2=0$ dhe $\displaystyle {{x}^{2}}+{{y}^{2}}-1=0$ . Të shkruhet ekuacioni i drejtëzës që bashkon qëndrat e tyre.