Pozicioni i dy drejtezave ne hapesire | Matematika 11

Pozicioni reciprok i dy drejtezave ne hapesire

Marrim në shqyrtim kuboidin ABCDMNPQ.

Duke i konsideruar brinjët e tij si drejtëza në hapësirë paraqiten këto raste:

Drejtëzat AB dhe DC ndodhen në një plan dhe nuk kanë asnjë pikë të përbashkët. Ato janë drejtëza paralele.
Drejtëzat AB dhe AD ndodhen në një plan dhe kanë pikën A të përbashkët. Ato janë drejtëza prerëse.
Drejtëzat AB dhe PC nuk ndodhen në një plan. Vëmë re se ato nuk kanë asnjë pikë të përbashkët. Dy drejtëza që nuk ndodhen në një plan quhen të kithëta.

Pozicioni reciprok i drejtëzës me planin

Në lidhje me një plan $\displaystyle \alpha$ , drejtëza d mund të ketë tri pozicione të ndryshme:

Drejteza d shtrihet në planin $\displaystyle \alpha$ . Shkruajmë $\displaystyle d\subset \alpha$ .

Drejtëza d dhe plani $\displaystyle \alpha$ kanë vetëm një pikë të përbashkët. Në këtë rast drejtëza d e pret planin $\displaystyle \alpha$ . Shkruajmë $\displaystyle d\cap \alpha =A$

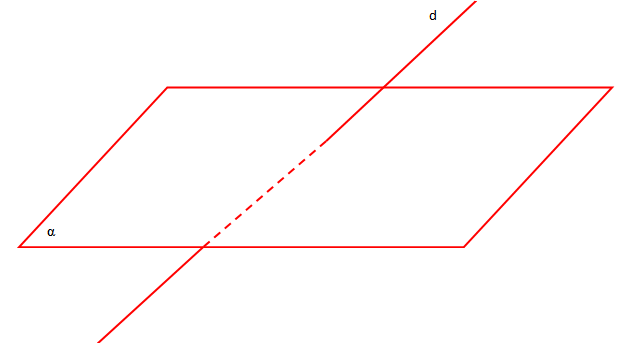
Drejtëza d dhe plani $\displaystyle \alpha$ nuk kanë asnjë pikë të përbashkët. Në këtë rast drejtëza është paralele me planin $\displaystyle \alpha$ . Shkruajmë $\displaystyle d//\alpha$ .

Drejteza pingule me planin

Teorema 1: “Në qoftë se një drejtëz është pingule me dy drejtëza të planit, të cilat kalojnë nga pika e prerjes, atëherë ajo është pingule me çdo drejtëz tjetër të planit, që kalon nga pika e prerjes”.

Shkruajmë

*** QuickLaTeX cannot compile formula:
\displaystyle \left[ d\bot a\ëedge d\bot b \right]\Rightarrow d\bot c

*** Error message:
Undefined control sequence \
leading text: $\displaystyle \left[ d\bot a\

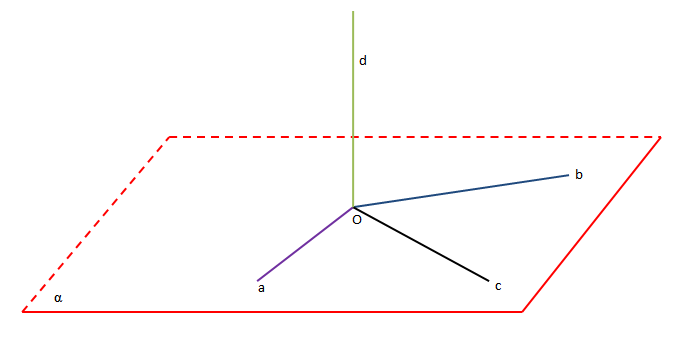
Këtë teoremë do ta pranojmë pa vërtetim.

Përkufizim: “Drejtëza d quhet pingule me planin, në qoftë se ajo është pingule me çdo drejtëz të tij, e cila kalon nga pika e prerjes”.

Duke u bazuar në teoremën e mësipërme, drejtëza është pingule me planin, në qoftë se ajo është pingule me dt drejtëza të planit, të cilat kalojnë nga pika e prerjes.

E pjerrëta dhe projeksioni i saj mbi plan

Drejtëza, e cila pret planin dhe nuk është pingule me të quhet e pjerrët ndaj planit.

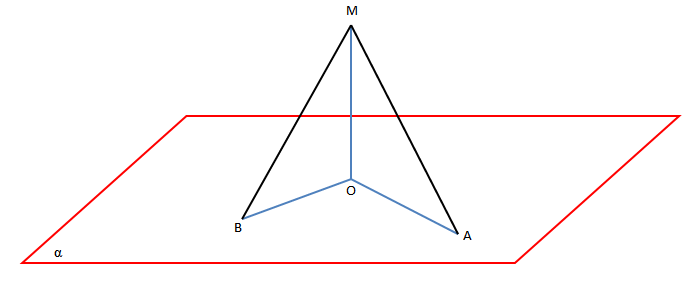
Mo është pingule me planin, ndërsa MA dhe MB janë të pjerrëta. Pika O quhet këmba e pingules, ndërsa pika A quhet këmba e të pjërrëtës MA.

Segmenti Oa, i cili bashkon këmbën e pingules me këmbën e të pjerrëtës quhet projeksion i të pjërrëtës në planin a.

Teorëmë: Në qoftë se nga një pikë M, ndërtojmë ndaj një plani pingulen MO dhe dy të pjerrëta MA dhe MB, atëherë:

Gjatësia e pignules është më e vogël se gjatësia e çdo të pjerrëte.
Në qoftë se të pjerrëtat janë të barabarta, atëherë edhe projeksionet e tyre janë të tilla.
Në qoftë se projeksionet e dy të pjerrëtave janë të barabarta, atëherë edhe të pjerrëtat janë të tilla.

Largesa e pikës nga plani

Largesë e pikës M nga plani a quhet segmenti i pingules së hequr nga pika M në planin α.

Këndi i të pjerrëtës me planin

Kënd i të pjerrëtës MA me planin α quhet këndi që kjo formon me projeksionin e saj në këtë plan.