Monotonia. Funksioni rrites dhe zbrites | Matematika 10

Funksioni rrites ne A

Përkufizim 1: “Funksioni numerik quhet rrites në bashkësinë A nëse për çdo çift numrash $\displaystyle {{x}_{1}},{{x}_{2}}\in A$ nga mosbarazimi $\displaystyle {{x}_{2}}>{{x}_{1}}$ rrjedh mosbarazimi $\displaystyle f\left( {{x}_{2}} \right)>f\left( {{x}_{1}} \right)$ ”.

$\displaystyle {{x}_{2}}>{{x}_{1}}\Rightarrow f\left( {{x}_{2}} \right)>f\left( {{x}_{1}} \right)$ për çdo çift numrash $\displaystyle {{x}_{1}},{{x}_{2}}\in A$ .

Pra, nga dy pika çfarëdo të grafikut, ajo që ka abshisën më të madhe, ka edhe ordinatën më të madhe.

Grafiku i funksionit rrites në bashkësinë A është në një vijë që ngjitet kur lëvizim djathtas.

Shembull

Më poshtë është dhënë grafiku i funksionit numerik f, me bashkësi përcaktimi $\displaystyle \left[ -1,3 \right]$

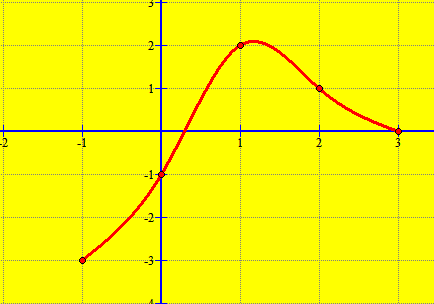
Ky funksion është rritës në segmentin $\displaystyle \left[ -1,1 \right]$ , por jo s=në segmentin $\displaystyle \left[ 1,3 \right]$ .

Funksioni $\displaystyle {{x}_{2}}>{{x}_{1}}$ është i njëvlershëm me $\displaystyle {{x}_{2}}-{{x}_{1}}>0$ , kurse $\displaystyle f\left( {{x}_{2}} \right)>f\left( {{x}_{1}} \right)$ është i njëvlershëm me $\displaystyle f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)>0$ .

Nëse funksioni është rritës në A, atëherë nga $\displaystyle {{x}_{2}}-{{x}_{1}}>0$ rrjedh $\displaystyle f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)>0$ dhe si pasojë raporti $\displaystyle \frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}$ është pozitiv, pra $\displaystyle \frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}>0$ .

Anasjelltas: Nëse $\displaystyle \frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}>0$ , nga mosbarazimi $\displaystyle {{x}_{2}}-{{x}_{1}}>0$ rrjedh $\displaystyle f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)>0$ , d.m.th funksioni f është rrites në A.

Kështu, kemi vërtetuar këtë teoremë:

Funksioni numerik është rritës në bashkësinë A atëherë dhe vetëm atëherë kur raporti $\displaystyle \frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}$ është pozitiv për çdo çift numrash $\displaystyle {{x}_{1}},{{x}_{2}}\in A\left( {{x}_{1}}\ne {{x}_{2}} \right)$ .

Teoremë: Funksioni linear $\displaystyle f:y=ax+b$ , kur $\displaystyle a>0$ është rrites në R.

Funksioni zbrites ne A

Përkufizim 2: “Funksioni numerik f quhet zbritës në bashkësinë A nëse për çdo çift numrash $\displaystyle {{x}_{1}},{{x}_{2}}\in A$ nga mosbarazimi $\displaystyle {{x}_{2}}>{{x}_{1}}$ rrjedh mosbarazimi $\displaystyle f\left( {{x}_{2}} \right)<f{{\left( x \right)}_{1}}$ ”. Për funksionin zbritës, me rritjen e vlerave të ndryshorit x, vlerat përgjegjëse të funksionit zvogëlohen.

Ndër dy pika çfarëdo të grafikut të tij, ajo që ka abshisën më të madhe, ka ordinatën më të vogël.

Teoremë: Funksioni f është zbritës në bashkësinë A atëherë dhe vetëm atëherë kur raporti $\displaystyle \frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}$ është negativ për çdo çift numrash $\displaystyle {{x}_{1}},{{x}_{2}}\in A\left( {{x}_{1}}\ne {{x}_{2}} \right)$ .

Teoremë: Funksioni linear $\displaystyle f:y=ax+b$ kur $\displaystyle a<0$ është zbritës në R. Funksioni që është rrites ose zbritës në bashkësinë A quhet funksion monoton në A.

Përkufizim 3: “Funksioni numerik që i ka të gjitha vlerat të barabarta quhet funksion konstant”.