Funksioni | Grafiku i funksionit | Matematika 9

Grafiku i funksionit $\displaystyle y=a{{x}^{2}}$

Monomi $\displaystyle y=a{{x}^{2}}$ (ku a është një numër real i ndryshëm nga zero), për çdo vlerë të x, ka një vlerë të caktuar reale. Prandaj, me anë të formulës $\displaystyle y=a{{x}^{2}}$ , $\displaystyle x\in R$ është një bashkësi e pafundme pikash.

Shembull 1

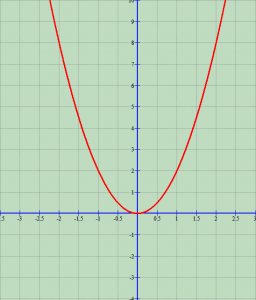
Ndërtoni grafikun e funksionit $\displaystyle y=2{{x}^{2}}$

Zgjidhje

Ndërtojmë në fillim tabelën e vlerave.

x	-2	-1	0	1	2	3
$\displaystyle y=2{{x}^{2}}$	8	2	0	2	8	18

Tani ndërtojmë grafikun e funksionit.

Shembull 2

Ndërtoni grafikun e funksionit $\displaystyle y=\frac{1}{2}{{x}^{2}}$

Zgjidhje

Ndërtojmë në fillim tabelën e vlerave.

x	-2	-1	0	1	2	3
$\displaystyle y=\frac{1}{2}{{x}^{2}}$	2	$\displaystyle \frac{1}{2}$	0	$\displaystyle \frac{1}{2}$	4	$\displaystyle \frac{9}{2}$

Tani ndërtojmë grafikun e funksionit.

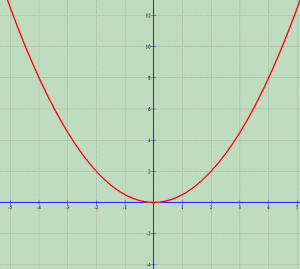
Përfundim: “Grafiku i funksionit $\displaystyle y=a{{x}^{2}}$ , $\displaystyle x\in R$ (ku a>0) është një vijë e përkulur (parabolë). Ajo ka si bosht simetrie boshtin Oy dhe si kulm origjinën O. Kjo parabolë ndodhet në gjysmëplanin e sipërm koordinativ dhe dëgët e saj shkojnë lart pambarimisht”.

Grafiku i funksionit $\displaystyle y=a{{x}^{2}}+n$

Le të ndërtojmë grafikun e funksionit $\displaystyle y=2{{x}^{2}}+2$ , $\displaystyle x\in R$ .

Plotësojmë tabelën

x	-2	-1	0	1	2	3
$\displaystyle y=2{{x}^{2}}$	8	2	0	2	8	18
$\displaystyle y=2{{x}^{2}}+2$	10	4	2	4	10	20

Tani ndërtojmë grafikun e funksionit

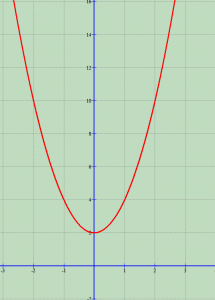
Përfundim: “Grafiku i funksionit $\displaystyle y=a{{x}^{2}}+n$ merret prej grafikut të funksionit $\displaystyle y=a{{x}^{2}}$ me zhvendosjen paralele me vektor $\displaystyle n\vec{j}$ . Ai është parabolë me bosht simetrie boshtin Oy dhe me kulm pikën (0, n)”.

Grafiku i funksionit $\displaystyle y=a{{\left( x-m \right)}^{2}}$

Le të ndërtojmë grafikun e funksionit $\displaystyle y=2{{\left( x-1 \right)}^{2}}$ .

Plotësojmë tabelën

x	-2	-1	0	1	2
$\displaystyle y=2{{\left( x-1 \right)}^{2}}$	18	8	2	0	2

Tani ndërtojmë grafikun e funksionit

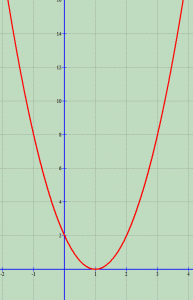
Përfundim: “Grafiku i funksionit $\displaystyle y=a{{\left( x-m \right)}^{2}}$ merret prej grafikut të funksionit $\displaystyle y=a{{x}^{2}}$ me zhvendosjen paralele me vektor $\displaystyle m\vec{i}$ . Ai është parabolë me kulm në pikën (m, 0) dhe me bosht simetrie drejtëzën x = m (paralele me boshtin Oy)”.

Grafiku i funksionit $\displaystyle y=a{{\left( x-m \right)}^{2}}+n$

Në mënyrë të ngjashme arrijmë në përfundimin: “Grafiku i funksionit $\displaystyle y=a{{\left( x-m \right)}^{2}}+n$ , $\displaystyle x\in R$ është një parabolë me kulm në pikën C(m,n) dhe me bosht simetrie drejtëzën me ekuacion x=m. Ai merret prej parabolës $\displaystyle y=a{{x}^{2}}$ me zhvendosje paralele me vektor $\displaystyle \vec{V}=m\vec{i}+n\vec{j}$ , që e çon origjinën në pikën C(m, n)”.

Funksioni $\displaystyle y=a{{x}^{2}}+bx+c$

Ne dimë që trinomi $\displaystyle a{{x}^{2}}+bx+c$ shndërrohet identikisht kështu:

$\displaystyle a{{x}^{2}}+bx+c=a{{\left( x+\frac{b}{2a} \right)}^{2}}-\frac{D}{4a}$ , ku $\displaystyle D={{b}^{2}}-4ac$ është dallori

Kështu, duke shënuar $\displaystyle \frac{-b}{2a}=m$ dhe $\displaystyle \frac{-D}{4a}=n$ ne marrim $\displaystyle a{{x}^{2}}+bx+c=a{{\left( x-m \right)}^{2}}+n$

Shembull 1

Zgjidhje

Shembull 2

Zgjidhje

Postime te ngjashme: