Vellimi i trupave gjeometrike | Vellimi i prizmit, piramides, cilindrit

Vëllimi i prizmit

Vellimi i prizmit është i barabartë me prodhimin e sipërfaqes së bazës me lartësinë e tij.

Gjithmonë tek prizmi i drejtë, lartësia është brinja e tij.

$\displaystyle V={{S}_{b}}\cdot l$

Ushtrim

Jepet prizmi me bazë trapez dhe lartësi 12 cm.
Baza e madhe e trapezit është 8 cm, baza e vogël është 4 cm, lartësia e trapezit është 6 cm dhe brinjët anësore jane nga 6 cm.

Gjeni:

a) Sipërfaqen anësore të prizmit

b) Sipërfaqen e bazës së prizmit

c) Sipërfaqen e përgjithshme të prizmit

d) Vëllimin e prizmit

Zgjidhje

Ndërtojmë në fillim prizmin me bazë trapez

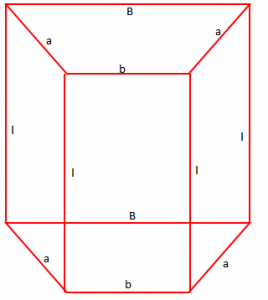
Kemi të dhënë:

l = 12 cm

B = 8 cm

b = 4 cm

h = 6 cm

a) Gjejmë sipërfaqen anësore

Nga formula dimë që:

$\displaystyle {{S}_{a}}=p\cdot l$

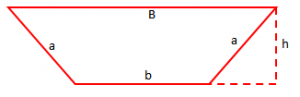
Gjejmë perimetrin e bazës, pra perimetrin e trapezit

P = 2a + b + B

P = 2 ∙ 6 + 4 + 8

P = 12 + 12

P = 24 cm

Tani gjejmë sipërfaqen anësore të prizmit me bazë trapez:

$\displaystyle {{S}_{a}}=p\cdot l$

$\displaystyle {{S}_{a}}=24\cdot 12$

$\displaystyle {{S}_{a}}=288c{{m}^{2}}$

b) Gjejmë sipërfaqen e bazës

Në fillim gjejmë sipërfaqen e trapezit:

$\displaystyle {{S}_{T}}=\frac{\left( B+b \right)\cdot h}{2}$

$\displaystyle {{S}_{T}}=\frac{\left( 8+4 \right)\cdot 6}{2}$

$\displaystyle {{S}_{T}}=12\cdot 3$

$\displaystyle {{S}_{T}}=36c{{m}^{2}}$

Tani për të gjetur sipërfaqen e bazës e shumëzojmë këtë sipërfaqe me 2:

$\displaystyle {{S}_{b}}=2\cdot 36$

$\displaystyle {{S}_{b}}=72c{{m}^{2}}$

c) Gjejmë sipërfaqen e përgjithshme

Nga formula, dimë që:

$\displaystyle {{S}_{p}}={{S}_{a}}+{{S}_{b}}$

Pra, do të kemi:

$\displaystyle {{S}_{p}}=288+72$

$\displaystyle {{S}_{p}}=360c{{m}^{2}}$

d) Gjejmë vëllimin e prizmit

Nga formula dimë që:

$\displaystyle {{V}_{p}}={{S}_{b}}\cdot l$ (sipërfaqen e njërës bazë).

Pra, do të kemi prodhimin e sipërfaqes së trapezit me lartësinë e prizmit:

$\displaystyle {{V}_{p}}=36\cdot 12$

$\displaystyle {{V}_{p}}=432c{{m}^{3}}$

Në rastin kur prizmi është kuboid, vellimi gjendet duke shumëzuar tri përmasat e kuboidit. Pra, $\displaystyle V=a\cdot b\cdot c$ .

Për kubin kemi a = b = c dhe $\displaystyle V={{a}^{3}}$ .

Shembull

Gjeni vëllimin e kuboidit me përmasa 3, 4 dhe 5 cm.

Zgjidhje

Nga formula, dimë që vellimi i kuboidit gjendet duke shumëzuar tri përmasat e tij. Pra, do të kemi:

$\displaystyle V=3\cdot 4\cdot 5=60c{{m}^{3}}$ .

Vellimi i piramidës

Vellimi i piramidës është sa $\displaystyle \frac{1}{3}$ e vëllimit të prizmit, ndaj shkruajmë:

$\displaystyle V=\frac{1}{3}{{S}_{b}}\cdot l$

Shembull

Gjeni vëllimin e piramidës me bazë drejtkëndësh, brinjët e të cilës janë 3 dhe 7 cm si dhe lartësia e piramidës është 10 cm.

Zgjidhje

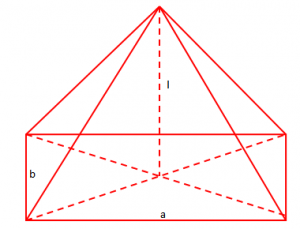
Për të gjetur vëllimin e piramidës, në fillim gjejmë sipërfaqen e bazës së saj. Nga formula e drejtkëndëshit, dimë që:

$\displaystyle {{S}_{b}}=a\cdot b$

$\displaystyle {{S}_{b}}=3\cdot 7=21c{{m}^{2}}$

Tani gjejmë vëllimin e piramidës:

$\displaystyle V=\frac{1}{3}{{S}_{b}}\cdot l$

$\displaystyle V=\frac{1}{3}21\cdot 10$

$\displaystyle V=7\cdot 10=70c{{m}^{3}}$

Vellimi i cilindrit

Ashtu si tek prizmi, edhe tek cilindri veprohet njësoj për gjetjen e vëllimit.

Pra, vëllimi i cilindrit është i barabartë me prodhimin e sipërfaqes së njërës bazë me lartësinë e tij.

$\displaystyle V={{S}_{b}}\cdot l$

Ne dimë $\displaystyle S=\pi {{R}^{2}}$ , kështu bëjmë zëvëndësimet dhe do të kemi:

$\displaystyle V=\pi {{R}^{2}}l$

Ushtrimi 1

Jepet cilindri me rreze 5 cm dhe lartësi 10 cm.

Gjeni vëllimin e cilindrit.

Zgjidhje

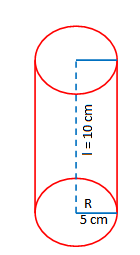
Nga formula dimë që:

$\displaystyle V=\pi {{R}^{2}}l$

Bëjmë zëvëndësimet:

$\displaystyle V=3,14\cdot {{5}^{2}}\cdot 10$

$\displaystyle V=3,14\cdot 25\cdot 10$

$\displaystyle V=3,14\cdot 250$

$\displaystyle V=750c{{m}^{3}}$