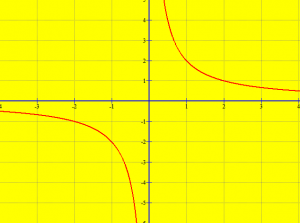
Funksioni perpjesetimor i zhdrejte | Matematika 8

Përkufizim: **“Grafiku i funksionit $\displaystyle y=\frac{a}{x}$ , $\displaystyle x\in {{Q}^{*}}$ përbëhet nga pika që ndodhen në një hiperbolë**”.

Kur a > 0, grafiku i funksionit perpjesetimor të zhdrejte $\displaystyle y=\frac{a}{x}$ , $\displaystyle x\in {{Q}^{*}}$ e ka njërën pjesë në kuadratin e parë dhe tjetrën n kuadratin e tretë.

Për shembull kemi funksionin $\displaystyle y=\frac{2}{x}$

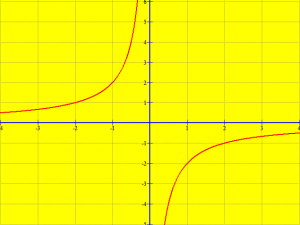
Kur a < 0, grafiku i funksionit perpjesetimor të zhdrejte $\displaystyle y=\frac{a}{x}$ , $\displaystyle x\in {{Q}^{*}}$ e ka njërën pjesë në kuadratin e dytë dhe tjetrën n kuadratin e katërt.

Për shembull kemi funksionin $\displaystyle y=\frac{-2}{x}$

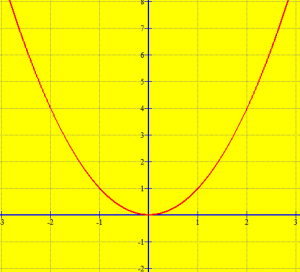
Funksioni $\displaystyle y={{x}^{2}}$

Përkufizim: “Grafiku i funksionit të dhënë me formulën $\displaystyle y={{x}^{2}}$ , $\displaystyle x\in Q$ , është një bashkësi pikash që ndodhen në një vijë që quhet parabolë”.

Ndërtojmë tabelën e vlerave të funksionit $\displaystyle y={{x}^{2}}$ .

x	-2	-1	0	1	2
y	4	1	0	1	4

Ndërtojmë grafikun e funksionit $\displaystyle y={{x}^{2}}$ .

Funksioni $\displaystyle y=a{{x}^{2}}$

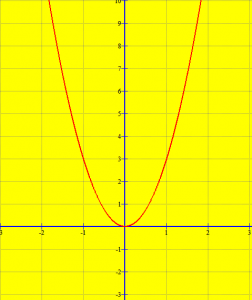
Përkufizim: “Grafiku i funksionit $\displaystyle y=a{{x}^{2}}$ , $\displaystyle x\in Q$ (ku a>0), është një vijë e përkulur (parabolë). Ajo ka si bosht simetrie boshtin Oy dhe si kulm origjinën O. Kjo parabolë ndodhet në gjysmëplanin e sipërm dhe degët e saj shkojnë lart pambarimisht”.

Shembull

Ndërtoni grafikun e funksionit $\displaystyle y=3{{x}^{2}}$

Zgjidhje

Ndërtojmë tabelën e vlerave të funksionit:

x	-2	-1	0	1	2
$\displaystyle y=3{{x}^{2}}$	-12	3	0	3	12

Ndërtojmë grafikun e funksionit:

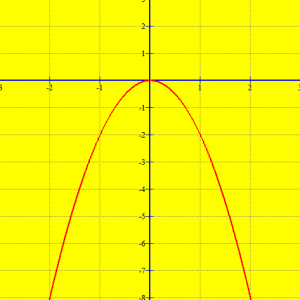
Përkufizim: “Grafiku i funksionit $\displaystyle y=a{{x}^{2}}$ , $\displaystyle x\in Q$ (ku a<0), është një vijë e përkulur (parabolë). Ajo ka si bosht simetrie boshtin Oy dhe si kulm origjinën O. Kjo parabolë ndodhet në gjysmëplanin e poshtëm dhe degët e saj shkojnë poshtë pambarimisht”.