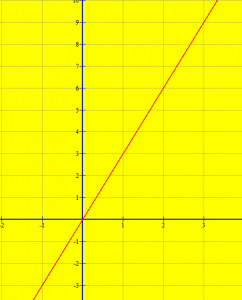
Grafiku i funksionit | Funksioni linear | Matematika 8

Përkufizim: “ Grafiku i funksionit numerik f në planin koordinativ xOy, quhet bashkësia e të gjitha pikave, që kanë si abshisa fytyrat (elementët e bashkësisë së përcaktimit), kurse si ordinatë kanë vlerat përgjegjëse të funksionit”.

Shembull 1

Të ndërtohet grafiku i funksionit të dhënë me formulën $\displaystyle y={{x}^{2}}-2$ , ku $\displaystyle x\in \left\{ -2,-1,0,1,2 \right\}$ .

Zgjidhje

Gjejmë për çdo vlerë të x vlerën përgjegjëse të funksionit dhe ndërtojmë pastaj tabelën.

Do të kemi:

x	-2	-1	0	1	2
y	2	-1	-2	-1	2

Atëherë pika të grafikut të funksionit janë:

A (-2, 2) ; B (-1, -1) ; C (0, -2); D (1, -1) ; F (2, 2)

Tani ndërtojmë grafikun e funksionit.

Në fillim ndërtojmë pikat në grafik:

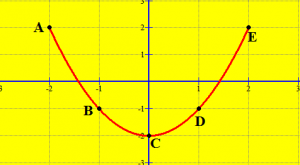
Tani bashkojmë pikat dhe formohet parabola:

Vërejtje: Në rast se nuk tregohet bashkësia e përcaktimit të funksionit të dhënë me formulë, do të nënkuptojmë që ajo është Q.

Funksioni linear

Përkufizim: “Funksioni i dhënë me formulën y= ax + b, ku a dhe janë numra të dhënë, kurse x është ndryshore që përshkon një bashkësi numerike, quhet funksion linear”.

Shembull

Të ndërtohet grafiku i funksionit $\displaystyle y=2x+1$ , $\displaystyle x\in Q$ .

Zgjidhje

Ndërtojmë tabelën me disa vlera të x dhe vlerat përgjegjëse te y.

x	-1	0	1	2	3	4
y	-1	1	3	5	7	9

Ndërtojmë çiftet e radhitura dhe më pas grafikun e funksionut:

A (-1, -1) ; B (0, 1) ; C (1, 3) ; D (2, 5) ; E (3, 7) ; F (4, 9)

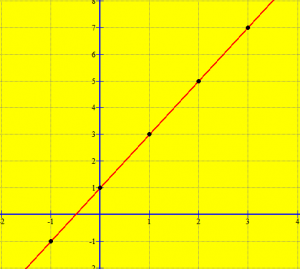
Vërtetohet (por ne do ta pranojmë pa vërtetim tani për tani) që grafiku i çdo funksioni linear është një bashkësi pikash që ndodhen në një drejtëz. Për ta vërtetuar këtë mjafton të gjejmë dy pika të saj, pra mjafton të gjejmë vlerat e funksionit për dy vlera të ndryshores.

Raste të veçanta të funksionit linear

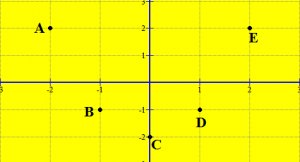
Rasti a = 0

Në këtë rast, funksioni y = ax + b merr formën y = b për çdo vlerë të x. Grafiku i tij është një bashkësi pikash që ndodhet në një drejtëz paralele me boshtin ox.