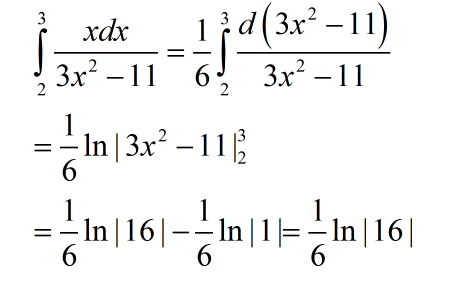
Integrali i caktuar | Veti te integralit te caktuar | Matematika 12

Përkufizimi i integralit të caktuar

Dimë se dy primitive të të njëjtit funksion f ndryshojnë nga njëri-tjetri me një konstante, pra $\displaystyle F\left( x \right)-G\left( x \right)=c$ .

Duke zëvëndësuar x=b dhe x=a, kemi:

$\displaystyle F\left( b \right)-G\left( b \right)=c$ dhe $\displaystyle F\left( a \right)-G\left( a \right)=c$ nga ku: $\displaystyle F\left( b \right)-G\left( b \right)=F\left( a \right)-G\left( a \right)$ ose $\displaystyle F\left( b \right)-F\left( a \right)=G\left( b \right)-G\left( a \right)$ .

Nga ky barazim del që për të gjetur diferencën $\displaystyle G\left( b \right)-G\left( a \right)$ mjafton të gjejmë diferencën $\displaystyle F\left( b \right)-F\left( a \right)$ , ku F është një primitiv çfarëdo i funksionit F.

Përkufizim: “Diferenca e njëjtë $\displaystyle F\left( b \right)-F\left( a \right)$ e vlerave të një primitivi çfarëdo F të funksionit f”.

Në pikat x=a dhe x=b quhet integral i caktuar i tij në segmentin $\displaystyle \left[ a,b \right]$ dhe shënohet me simbolin $\displaystyle \int\limits_{a}^{b}{f\left( x \right)dx}$ ).

Lexohet integrali i caktuar nga a në b i $\displaystyle f\left( x \right)dx$ . $\displaystyle a$ quhet kufiri i poshtëm i integrimit, kurse $\displaystyle b$ quhet kufiri i sipërm i integrimit.

Sipas këtij përkufizimi kemi:

$\displaystyle \int\limits_{a}^{b}{f\left( x \right)dx}=F\left( b \right)-F\left( a \right)$ .

Duke shënuar $\displaystyle F\left( b \right)-F\left( a \right)=F\left( x \right)|_{a}^{b}$ kemi:

$\displaystyle \int\limits_{a}^{b}{f\left( x \right)dx}=F\left( x \right)|_{a}^{b}=F\left( b \right)-F\left( a \right)$ . Ky quhet përkufizimi i integralit të caktuar.

Pra, për njehsimin e integralit të caktuar $\displaystyle \int\limits_{a}^{b}{f\left( x \right)dx}$ kryhen veprimet e mëposhtme:

Gjendet një primitiv çfarëdo F i funksionit f, dmth integral i pacaktuar i tij $\displaystyle \int{f\left( x \right)dx}$ .
Njehsohet diferenca $\displaystyle F\left( b \right)-F\left( a \right)=F\left( x \right)|_{a}^{b}$ e vlerave të funksionit $\displaystyle F\left( x \right)$ , për x=b dhe x=a.

Shembull 1

Të njehsohet integrali i caktuar $\displaystyle \int\limits_{0}^{1}{\left( {{x}^{2}}-x+1 \right)}dx$

Zgjidhje

$\displaystyle \int\limits_{0}^{1}{\left( {{x}^{2}}-x+1 \right)}dx=\left( \frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2}+x \right)|_{0}^{1}$

$\displaystyle =\left( \frac{{{1}^{3}}}{3}-\frac{{{1}^{2}}}{2}+1 \right)-\left( \frac{{{0}^{3}}}{3}-\frac{{{0}^{2}}}{2}+0 \right)$

$\displaystyle =\frac{2}{6}-\frac{3}{6}+\frac{6}{6}-0=\frac{5}{6}$

Veti të integralit të caktuar

Shumëzuesi konstant mund të dal jashtë shënjës së integralit të caktuar

$\displaystyle \int\limits_{a}^{b}{k\cdot f\left( x \right)dx}=k\cdot \int\limits_{a}^{b}{f\left( x \right)dx}$

Integrali i caktuar i shumës algjebrike të disa funksioneve të barabarta është i barabartë me shumën algjebrike të integraleve të caktuara të këtyre funksioneve.

$\displaystyle \int\limits_{a}^{b}{\left[ f\left( x \right)+g\left( x \right) \right]dx}=$

$= \int\limits_{a}^{b}{f\left( x \right)dx}+\int\limits_{a}^{b}{g\left( x \right)dx}$

Në qoftë se c është një pikë e segmentit $\displaystyle \left[ a,b \right]$ , atëherë:

$\displaystyle \int\limits_{a}^{b}{f\left( x \right)dx=}\int\limits_{a}^{c}{f\left( x \right)dx+\int\limits_{c}^{b}{f\left( x \right)dx}}$ .

Gjithashtu pranojmë me marrëveshje se:

$\displaystyle \int\limits_{a}^{a}{f\left( x \right)dx=}0$ dhe $\displaystyle \int\limits_{a}^{b}{f\left( x \right)dx=}-\int\limits_{b}^{a}{f\left( x \right)dx=}$ .

Ushtrime të zgjidhura

Ushtrimi 1

Të njehsohen integralet e caktuara:

a) $\displaystyle \int\limits_{0}^{2}{\frac{xdx}{{{x}^{2}}+4}}$

b) $\displaystyle \int\limits_{0}^{\frac{\pi }{2}}{\left( \cos 2x-\sin 4x \right)}dx$

Zgjidhje

a) $\displaystyle \int\limits_{0}^{2}{\frac{xdx}{{{x}^{2}}+4}}$

$\displaystyle \int\limits_{0}^{2}{\frac{xdx}{{{x}^{2}}+4}}=\frac{1}{2}\int\limits_{0}^{2}{\frac{d\left( {{x}^{2}}+4 \right)}{{{x}^{2}}+4}}$

$\displaystyle =\left( \frac{1}{2}\ln |{{x}^{2}}+4| \right)|_{0}^{2}$

$\displaystyle =\left( \frac{1}{2}\ln |8| \right)-\left( \frac{1}{2}\ln |4| \right)$

$\displaystyle =\frac{1}{2}\ln |2|$

b) $\displaystyle \int\limits_{0}^{\frac{\pi }{2}}{\left( \cos 2x-\sin 4x \right)}dx$

$\displaystyle \int\limits_{0}^{\frac{\pi }{2}}{\left( \cos 2x-\sin 4x \right)}dx=$

$\int\limits_{0}^{\frac{\pi }{2}}{\cos 2xdx-\int\limits_{0}^{\frac{\pi }{2}}{\sin 4xdx}}$

$\displaystyle =\frac{1}{2}\sin 2x|_{0}^{\frac{\pi }{2}}+\frac{1}{4}\cos 4x|_{0}^{\frac{\pi }{2}}$

$\displaystyle =\left( \frac{1}{2}\sin \pi -\frac{1}{2}\sin 0 \right)+$

$+ \left( \frac{1}{4}\cos 2\pi -\frac{1}{4}\cos 0 \right)$

$\displaystyle =\left( 0-0 \right)+\left( \frac{1}{4}\,-\frac{1}{4} \right)=0$ .

Ushtrimi 2

Të njehsohen integralet e caktuara:

a) $\displaystyle \int\limits_{0}^{1}{\left( 2x+3 \right)dx}$

b) $\displaystyle \int\limits_{0}^{2}{{{\left( 2x-4 \right)}^{2}}dx}$

c) $\displaystyle \int\limits_{1}^{2}{\frac{dx}{{{x}^{2}}}}$

d) $\displaystyle \int\limits_{2}^{3}{\frac{xdx}{3{{x}^{2}}-11}}$

Zgjidhje

a) $\displaystyle \int\limits_{0}^{1}{\left( 2x+3 \right)dx}$

$\displaystyle \int\limits_{0}^{1}{\left( 2x+3 \right)dx}=2\int\limits_{0}^{1}{xdx}+3\int\limits_{0}^{1}{dx}$

$\displaystyle =\left( 2\frac{{{x}^{2}}}{2}+3x \right)|_{0}^{1}$

$\displaystyle =\left( 1+3 \right)-\left( 0+0 \right)=4$

b) $\displaystyle \int\limits_{0}^{2}{{{\left( 2x-4 \right)}^{2}}dx}$

$\displaystyle \int\limits_{0}^{2}{{{\left( 2x-4 \right)}^{2}}dx}=\int\limits_{0}^{2}{\left( 4{{x}^{2}}-16x+16 \right)dx}$

$\displaystyle 4\int\limits_{0}^{2}{\left( {{x}^{2}}-4x+4 \right)dx}$

$\displaystyle =4\left( \frac{{{x}^{3}}}{3}-4\frac{{{x}^{2}}}{2}+4x \right)_{0}^{2}$

$\displaystyle =4\left( \frac{8}{3}-8+8 \right)-4\cdot 0$

$\displaystyle =\frac{32}{3}$

c) $\displaystyle \int\limits_{1}^{2}{\frac{dx}{{{x}^{2}}}}$

$\displaystyle \int\limits_{1}^{2}{\frac{dx}{{{x}^{2}}}}=-\frac{1}{x}|_{1}^{2}$

$\displaystyle =-\frac{1}{2}+1=\frac{1}{2}$

d) $\displaystyle \int\limits_{2}^{3}{\frac{xdx}{3{{x}^{2}}-11}}$

$\displaystyle \int\limits_{2}^{3}{\frac{xdx}{3{{x}^{2}}-11}}=\frac{1}{6}\int\limits_{2}^{3}{\frac{d\left( 3{{x}^{2}}-11 \right)}{3{{x}^{2}}-11}}$

$\displaystyle =\frac{1}{6}\ln |3{{x}^{2}}-11|_{2}^{3}$

$\displaystyle =\frac{1}{6}\ln |16|-\frac{1}{6}\ln |1|=\frac{1}{6}\ln |16|$