
Provimi i lirimit 2018– Matematike (ushtrimet e zgjidhura me zhvillim)
Këtu do të trajtojmë pyetjet me zhvillim që kanë rënë tek provimi i lirimit në qershor 2018.
Zgjidhja e ushtrimeve të provimit të lirimit 2018 do t’ju ndihmojë në përgatitjen e provimit të lirimit për vitet në vijim.
Ushtrimi 14
a) Të zgjidhet ekuacioni
b) Të zgjidhet inekuacioni
Zgjidhje
a)
Në fillim zbërthejmë katrorin e binomit:
Duke bërë thjeshtimet do të kemi:
Bëjmë faktorizimin:
Do të kemi:
b) Në fillim shumëzojmë me 3 të dyja krahët në mënyrë që të heqim emëruesin:
Pra, bashkësia e vlerave të x është .
Ushtrimi 15
Thjeshtoni shprehjen
Zgjidhje
I shkruajmë fuqitë në formë prodhimi:
Tani bëjmë faktorizime:
Ushtrimi 16
Jepet trapezi ABCD me diagonale AC = 13 cm dhe BD = 15 cm dhe lartësi 12 cm. Gjeni sipërfaqen e tij.
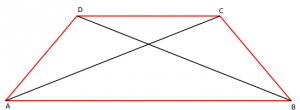
Zgjidhje
Në fillim zgjasim DC në mënyrë të tillë që CE = AB dhe EB // AC.
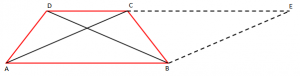
Pra, kemi ABEC paralelogram, ku AC = BE dhe AB = CE.
Formulën mund ta zëvëndësojmë
ose
.
Ndërtojmë lartësinë e trapezit.
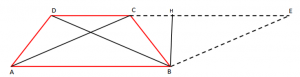
Me anë të teoremës së Pitagorës gjejmë DH dhe HE.
Pra, DE = HD + HE = 9 + 5 = 14 cm.
Tani gjejmë sipërfaqen:
Ushtrimi 17
Perimetri i një drejtkëndëshi është 250 m. gjatësia e tij është 5 m më e madhe se 3-fishi i gjerësisë.
Gjeni syprinën e drejtkëndëshit.
Zgjidhje

Kemi drejtkëndëshin me gjatësi a dhe gjerësi b.
Kemi:
P = 250 m
Formojmë ekuacionin:
Bëjmë zëvëndësimet:
Tani gjejmë gjatësine a:
Gjejmë sipërfaqen e drejtkëndëshit:
Ushtrimi 18
Të zgjidhet sistemi 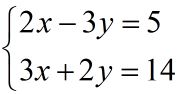
Zgjidhje
Për zgjidhjen e sistemit përdorim mënyrën me zëvëndësim:
Veçojmë x-in tek ekuacioni i parë:
E zëvëndësojmë x-in tek ekuacioni i dytë:
Pjestojmë me 2 të dy anët:
Tani zëvëndësojmë vlerën e y-it tek ekuacioni i parë:
Pra, zgjidhje e sistemit është çifti i radhitur (4, 1).
Ushtrimi 19
Jepet funksioni .
a) Gjeni pikën në grafik me abshisë 1
b) Gjeni pikën në grafik me ordinatë 2
Zgjidhje
E shkruajmë funksionin ne trajtën .
a) Zëvëndësojmë x-in me 1 dhe gjejmë y-in:
Pra, pika në grafik më abshisë 1 në funksionin është pika (1, 2)
b) Zëvëndësojmë y-in me 2 dhe gjejmë x-in:
E shkruajmë në trajtë të rregullt:
Gjejmë dallorin:
, pra ekuacioni ka dy zgjidhje.
Pikat në grafik me ordinatë 2 në funksionin janë pikat (1,2 ) dhe (2, 2).
Ushtrimi 20
Në një trekëndësh kënddrejtë lartësia mbi hipotenuzë është 6 cm dhe projeksioni i njërit katet është mbi hipotenuzë është 8 cm.
a) Gjeni gjatësinë e këtij kateti
b) Gjeni hipotenuzën dhe katetin tjetër
Zgjidhje
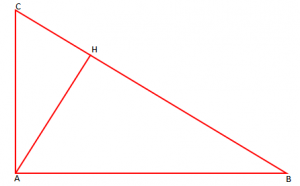
a) Kemi AH = 6 cm dhe BH = 8 cm.
Gjejmë katetin AB në bazë të teoremës së Pitagorës:
.
b) Për të gjetur hipotenuzën BC zbatojmë teoremën e dytë të Euklidit:
Për të gjetur katetin tjetër përdorim teoremën e Pitagorës:
Ushtrimi 21
Të thjeshtohet thyesa
Zgjidhje
Përdorim faktorizimet:
Ushtrimi 22
Brinjët e një trekëndëshi rrinë si 4:5:6. Perimetri i një trekëndëshi të ngjashëm me të është 45 cm. Gjeni brinjët e trekëndëshit të dytë.
Zgjidhje
Brinjët e trekëndëshit të parë rrinë 4x : 5x : 6x.
Brinjët e trekëndëshit të dytë rrinë 4xk : 5xk : 6xk.
4xk + 5xk + 6xk=45
15xk=45
xk=3
Tani zëvëndësojmë xk tek brinjët e trekëndëshit të dytë dhe do të kemi:
Ushtrimi 23
Shuma e katër numrave të njëpasnjëshëm është 38.
a) Gjeni mesataren e tyre
b) Gjeni numrat
Zgjidhje
a) Për të gjetur mesataren mjafton të pjesëtojmë shumën e numrave me 4. Pra:
b) Për të gjetur numrat, në fillim formojmë ekuacionin:
Numri i parë është 8, ndërsa numrat e tjerë janë 9, 10 dhe 11.
Ushtrimi 24
Për ç’vlerë të a ekuacioni nuk ka rrënjë reale?
Zgjidhje
Duhet që . Pra,
. Bëjmë zëvëndësimet:
Tani bëjmë studimin e shenjës:
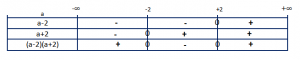
Pra, për ]-2, 2[ ekuacioni nuk ka rrënjë reale.
Ushtrimi 25
Gjeni bashkësinë e vlerave të palejuara të x në shprehjen .
Zgjidhje
Dimë që shprehja nën rrënjë duhet të jetë më e madhe ose e barabartë me zero. Pra:
.
Formojmë sistemin e inekuacioneve:
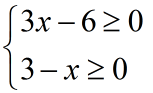
Zgjidhim inekuacionin e dyfishtë:
![]()
Mund të shikoni gjithashtu Provimi i lirimit 2018 – Matematike (Alternativa)

