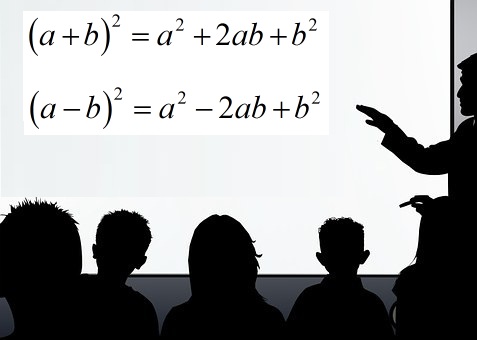
Katrori i binomit | Faktorizime me faktorin e binomit

Katrori i binomit shkruhet në formën: $\displaystyle {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$

Vërtetojmë identitetin:

$\displaystyle {{\left( a+b \right)}^{2}}=\left( a+b \right)\cdot \left( a+b \right)$

Shumëzojmë kllapat:

$\displaystyle \left( a+b \right)\cdot \left( a+b \right)={{a}^{2}}+ab+ab+{{b}^{2}}$

Reduktojmë kufizat e ngjashme:

$\displaystyle ={{a}^{2}}+2ab+{{b}^{2}}$

Pra, u vërtetua identiteti:

$\displaystyle {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ .

Shembull 1

Gjeni:

a) $\displaystyle {{\left( x+4 \right)}^{2}}$

b) $\displaystyle {{\left( 3x+9 \right)}^{2}}$

Zgjidhje

a) $\displaystyle {{\left( x+4 \right)}^{2}}$

$\displaystyle {{\left( x+4 \right)}^{2}}={{x}^{2}}+2\cdot 4x+{{4}^{2}}$

$\displaystyle ={{x}^{2}}+8x+16$

b) $\displaystyle {{\left( 3x+9 \right)}^{2}}$

$\displaystyle {{\left( 3x+7 \right)}^{2}}={{\left( 3x \right)}^{2}}+2\cdot 3x\cdot 7+{{7}^{2}}$

$\displaystyle =9{{x}^{2}}+42x+49$

Kemi gjithashtu dhe identitetin: $\displaystyle {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$ .

Vërtëtim. Njësoj si në rastin e parë edhe këtë herë do zbërthejmë shprehjen në faktorë.

$\displaystyle {{\left( a-b \right)}^{2}}=\left( a-b \right)\left( a-b \right)$

Shumëzojmë shprehjet në kllapa:

$\displaystyle ={{a}^{2}}-ab-ab+{{b}^{2}}$

Reduktojmë kufizat e ngjashme:

$\displaystyle ={{a}^{2}}-2ab+{{b}^{2}}$

Shembull 2

Zbërtheni $\displaystyle {{\left( 3x-5y \right)}^{2}}$

Zgjidhje

$\displaystyle {{\left( 3x-5y \right)}^{2}}={{\left( 3x \right)}^{2}}-2\cdot 3x\cdot 5y+{{\left( 5y \right)}^{2}}$

$\displaystyle =9{{x}^{2}}-30xy+25{{y}^{2}}$

Faktorizimi me anë të formulës së katrorit të binomit

Duke ndërruar vendet e të dyja anëve në identitet për $\displaystyle {{\left( a+b \right)}^{2}}$ ne mund të shkruajmë:

$\displaystyle {{a}^{2}}+2ab+{{b}^{2}}={{\left( a+b \right)}^{2}}$

$\displaystyle {{a}^{2}}-2ab+{{b}^{2}}={{\left( a-b \right)}^{2}}$

Këto dy identitete na lejojnë të bëjmë zbërthime në faktorë të shprehjeve që kanë trajtën $\displaystyle {{a}^{2}}+2ab+{{b}^{2}}={{\left( a+b \right)}^{2}}$ ose $\displaystyle {{a}^{2}}-2ab+{{b}^{2}}={{\left( a-b \right)}^{2}}$ .

Shembull 1

Zbërtheni në faktorë:

a) $\displaystyle 4{{x}^{2}}+12x+9$

b) $\displaystyle 16{{x}^{2}}-16x+4$

Zgjidhje

a) $\displaystyle 4{{x}^{2}}+12x+9$

Vëmë re se kufiza e parë është katrori i shprehjes 2x, kurse e treta katrori i numrit 3.

Kufiza e dytë është dyfishi i prodhimit të kufizës së parë me kufizën e tretë, pra $\displaystyle 12=2\cdot 3\cdot 2$ , ndaj mund të faktorizojmë:

$\displaystyle 4{{x}^{2}}+12x+9={{\left( 2x+3 \right)}^{2}}$

b) $\displaystyle 16{{x}^{2}}-16x+4$

Në të njëjtën mënyrë veprojmë dhe në këtë rast dhe do të kemi:

$\displaystyle 16{{x}^{2}}-16x+4=\left( 4x-2 \right)$

Shembull 1

Zgjidhje

Shembull 2

Faktorizimi me anë të formulës së katrorit të binomit

Shembull 1

Zgjidhje

Postime te ngjashme: