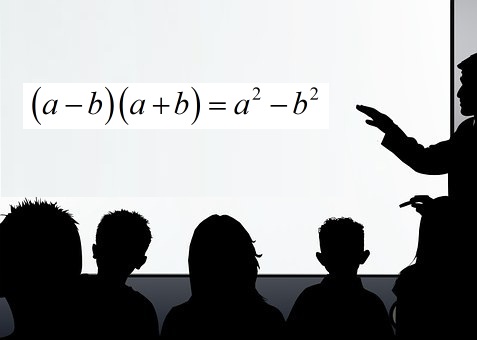
Ndryshesa e katroreve shkruhet:
Le të vërtetojmë identitetin.
Zbatojmë vetinë e përdasimit:
Reduktojmë kufizat e ngjashme:
Identiteti u vërtetua. Ky identitet na lejon të kryejmë shkurt shumëzimin e shumë së dy shprehjeve me ndryshesën e tyre.
Shembull 1
Paraqitini shkurt, si polinom prodhimet:
a)
b)
c)
Zgjidhje
a)
Nga ndryshesa e katroreve, do të kemi:
b)
Nga ndryshesa e katroreve, do të kemi:
c)
Nga ndryshesa e katroreve, do të kemi:
Shembull 2
Të paraqiten shkurt si polinom shprehjet:
a)
b)
c)
Zgjidhje
a)
e shkruajmë ndryshe
dhe do të kemi:
Nga ndryshesa e katrorevedo të kemi:
b)
Në të njëjtën mënyrë veprojmë dhe në këtë rast. Do të kemi:
c)
Në fillim faktorizojmë prodhimin:
Reduktojmë kufizat e ngjashme:
Formulën e quajmë formulë e ndryshesës së katroreve dhe përdoret për për të zbëerthyer në faktorë ndryshesën e katrorëve të dy shprehjeve.
Ushtrimi 1
Zbertheni në faktorë:
a)
b)
c)
Zgjidhje
a)
Në fillim i kthejmë të dy kufizat si fuqi të dyshit:
Nga formula e ndryshesës së katrorit, do të kemi:
b)
Në fillim i kthejmë të dy kufizat si fuqi të dyshit:
Nga formula e ndryshesës së katrorit, do të kemi:
c)
Në fillim i kthejmë të dy kufizat si fuqi të dyshit:
Nga formula e ndryshesës së katrorit, do të kemi:

