Simetria sipas një pike quhet ndryshe dhe simetria qëndrore.

 

 

Simetria e një pike në lidhje me një pikë

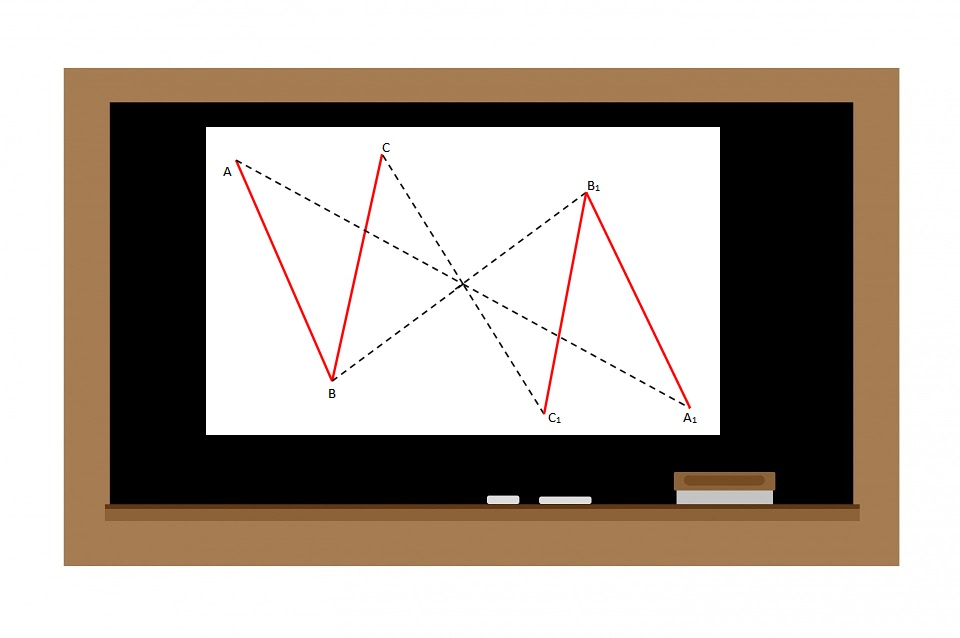
• Marrim në plan një pikë O dhe një pikë çfarëdo A.
• Bashkojmë me gjysmëdrejtëz pikën A me pikën O.
• Marrim

Pika A₁ quhet simëetrike e pikës A në lidhje me pikën O.

Anasjelltas

Marrim pikën simetrike të pikës A₁ në lidhje me pikën O. Do të kemi pikën A.

Tani mund të themi që pika A dhe A₁ janë simetrike të njera – tjetrës në lidhje me pikën O.

Pika O quhet qëndër simetrie.

 

Përkufizim: “Dy pika A dhe A₁ quhen simetrike në lidhje me një pikë O , nëse pika O është në mes të segmentit AA₁”.

 

 

 

Simetria e një segmenti në lidhje më një pikë

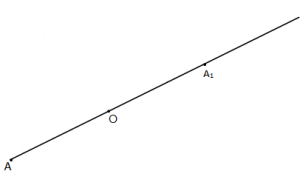
• Marrim një segment çfarëdo AB dhe një pikë çfarëdo O.
• Meqë skajet e segmentit AB janë pikat A dhe B, si më sipër, gjejmë simetriket e A dhe B sipas pikës O dhe dalin Pikat A₁ dhe B₁.
• Bashkojmë pikat A₁ dhe B₁

Shohim figurën:

 

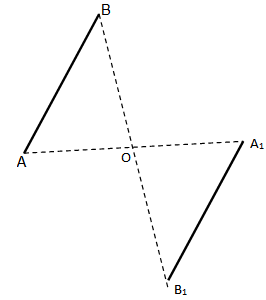
• Segmenti A₁ B₁ është simetriku i segmentit AB në lidhje me pikën O dhe shkruajmë:

Përkufizim: “Dy segmente simetrike në lidhje me një pikë janq kongruente dhe paralele”.

 

 

 

 

 

Simetria e një këndi në lidhje më një pikë

• Marrim një kënd çfarëdo dhe një pikë O si qëndër simetrie
• Ndërtojmë simetriken e kulmit A, pikës B dhe pikës C në lidhje me pikën O.
• Shënojmë A₁, B₁, C₁ simetriket e tyre.
• Bashkojmë A₁, B₁, C₁ në mënyrën që janq bashkuar A, B, C.

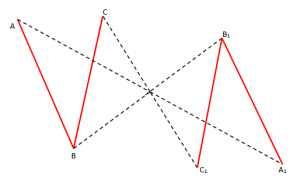
Përkufizim: “Dy kënde simetrike në lidhje me një pikë janë kongruentë”.

Pra,

dhe

 

 

 

 

Simetria e një figure në lidhje me një pikë

Figura mund të jetë trekëndësh, katërkëndësh (katërkëndësh, paralelogram etj), pesëkëndësh etj.

Kemi figurën më poshtë:

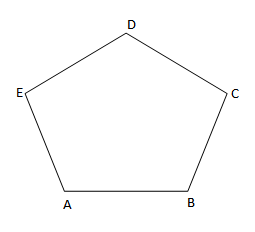
Marrim një pikë O jashtë saj.

Ndërtojmë me radhë simetriket e pikave A, B, C, D, E në lidhje me pikën O.

I shënojmë A₁, B₁, C₁, D₁, E₁ dhe i bashkojmë në të njëjtën mënyrë si janë bashkuar në figurën ABCDE dhe themi:

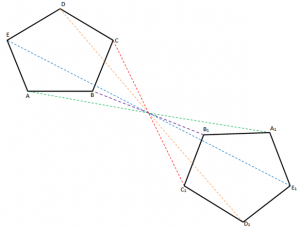
Përkufizim: “Dy figura simetrike në lidhje me një pikë janë kongruente”.