Veti të funksionit y = tgx
- Meqënëse
, ai ekziston vetëm për ato vlera x të harqeve AM, që e kanë
, domethënë për të cilat
.
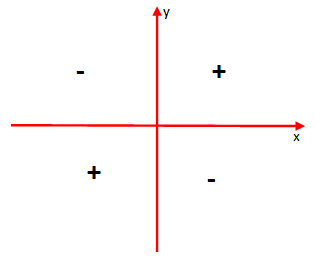
- Duke njohur shenjat e sinx, cosx dhe në bazë të formulës
, nxjerrim përfundimet e paraqitura në tabelën e mëposhtme, lidhur me shenjën e tgx, sipas kuadratit ku mbaron harku x.
- Shënojmë me t drejtëzën tangjente ndaj rrethit trigonometrik, hequr në pikën A. Marrim harkun trigonometrik AM me vlerë x dhe shënojmë me T pikën ku drejtëza
pret tangjenten t.
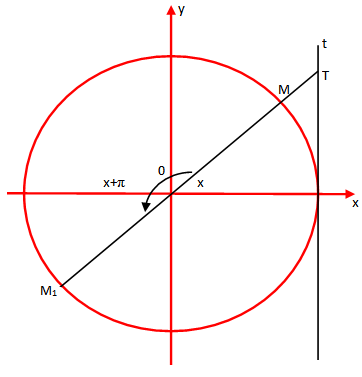
Vektorët dhe
janë bashkëvizorë, prandaj ekziston një numër k, i tillë që
.
Nga këtu del që:
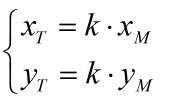
Pra, , pra
.
Por dhe
.
Meqë është ordinatë e pikës T, por edhe e vektorit AT, barazimi
shprehet kështu: “Në rrethin trigonometrik, tgx paraqitet gjeometrikisht nga vektori AT”.
- Funksioni y = tgx është funksion periodik me periodë π. Tregohet gjithashtu dhe që
,
.
Variacioni i funksionit y = tgx
Meqënëse ky funksion është periodik me periodë π, mjafton ta studiojmë atë në një segment me gjatësi π, saktësisht në segmentin .
Meqënëse y = tgx, mjafton të shqyrtojmë se si ndryshon ordinate e pikës T, kur x rritet nga drejt
, domethënë kur pika M lëviz në rrethin trigonometrik nga B’ në B.
Më poshtë kemi grafikun e funksionit y = tgx, . Grafiku i funksionit
merret duke përsëritur një sasi të pafundme herësh majtas e djathtas.
Ndërtojmë tabelën dhe grafikun e funksionit:
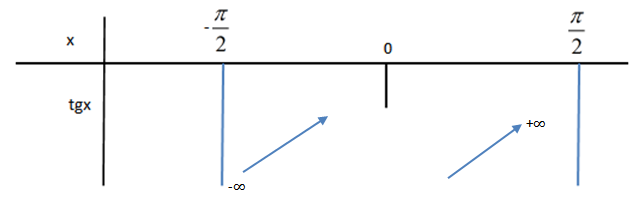
tabela e funksionit
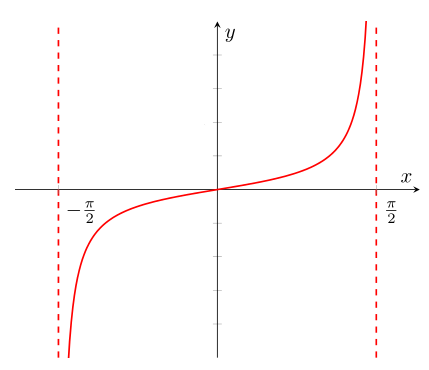
grafiku i funksionit

