Trinomi i fuqise se dyte me nje te panjohur | Matematika 10

Trinomi i fuqise se dyte me nje te panjohur

Përkufizim: “Shprehja $\displaystyle a{{x}^{2}}+bx+c$ quhet trinom i fuqisë së dytë me një të panjohur”.

$\displaystyle a{{x}^{2}}+bx+c$ është ana e majtë e ekuacionit $\displaystyle a{{x}^{2}}+bx+c=0$ .

Përkufizim: “Rrënjë të trinomit $\displaystyle a{{x}^{2}}+bx+c$ do të quajmë rrënjët e ekuacionit $\displaystyle a{{x}^{2}}+bx+c=0$ ”.

Studimi i shënjës së trinomit

Për të përcaktuar shënjën e trinomit veprojmë kështu:

Le të jenë $\displaystyle {{x}_{1}}\ne {{x}_{2}}$ (D>0) rrënjët e trinomit $\displaystyle a{{x}^{2}}+bx+c$ ( $\displaystyle {{x}_{1}}<{{x}_{2}}$ ). Faktorizojmë a-në:

$\displaystyle a{{x}^{2}}+bx+c=a\left( {{x}^{2}}+\frac{b}{a}x+\frac{c}{a} \right)$ .

Nga formulat e Vietës shkruajmë:

$\displaystyle {{x}_{1}}+{{x}_{2}}=-\frac{b}{a}$ dhe $\displaystyle {{x}_{1}}\cdot {{x}_{2}}=\frac{c}{a}$ .

I zëvëndësojmë tek formula më lart:

$\displaystyle a\left( {{x}^{2}}+\frac{b}{a}x+\frac{c}{a} \right)=a\left[ {{x}^{2}}-\left( {{x}_{1}}+{{x}_{2}} \right)x+{{x}_{1}}\cdot {{x}_{2}} \right]$ .

Kryejmë faktorizimin me grupe:

$\displaystyle a\left( {{x}^{2}}+\frac{b}{a}x+\frac{c}{a} \right)=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)$ .

Pra, kemi:

$\displaystyle a{{x}^{2}}+bx+c=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)$ .

Kemi tre raste:

Rasti i parë

$\displaystyle x>{{x}_{2}}\Leftrightarrow x-{{x}_{1}}>0$ dhe $\displaystyle x-{{x}_{2}}>0$ .

Nëse $\displaystyle a>0$ , atëherë $\displaystyle a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)>0$ .

Nëse $\displaystyle a<0$ , atëherë $\displaystyle a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)<0$ . Pra, prodhimi ka shënjën e a-së.

Rasti i dytë

$\displaystyle x<{{x}_{1}}\Leftrightarrow x-{{x}_{2}}<0$ .

Nëse $\displaystyle a>0$ , atëherë $\displaystyle a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)>0$ .

Nëse $\displaystyle a<0$ , atëherë $\displaystyle a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)<0$ . Pra, prodhimi ka shënjën e a-së.

Për këto dy raste del ky përfundim: Trinomi ka shënjën e a-së për të gjitha x-et jashtë rrënjëve.

Rasti i tretë

$\displaystyle x={{x}_{1}}$ ose $\displaystyle x={{x}_{2}}$ atëherë $\displaystyle a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)=0$ .

Përfundim: Për të gjitha x-et jashtë rrënjëve vlerat e trinomit kanë shënjën e a-së, për të gjitha x-et midis rrënjëve vlerat e trinomit kanë shënjën e kundërt të a-së dhe për x të barabarta me rrënjët trinomi merr vlerën zero.

Ndërtojmë tabelën per studimin e shënjës së trinomit.

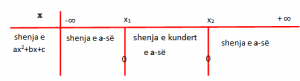
Le të jetë $\displaystyle {{x}_{1}}={{x}_{2}}$ (D=0) rrënja e trinomit $\displaystyle a{{x}^{2}}+bx+c=a{{\left( x-{{x}_{1}} \right)}^{2}}$ .

Ana e djathtë e barazimit tregon se për çdo vlerë $\displaystyle x\ne {{x}_{1}}$ vlerat e trinomit kanë shënjën e a-së dhe për $\displaystyle x={{x}_{1}}=-\frac{b}{2a}$ , pra për rrënjën, trinomi merr vlerën zero.

Ndërtojmë tabelën për studimin e shënjës së trinomit.

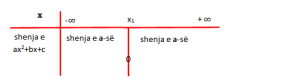
Vërtetohet se trinomi nuk ka rrënjë reale (D<0), për çdo x reale mmerr vlera që kanë shënjës e a-së.

Përfundim

Nëse D>0 trinomi për të gjitha x jashtë rrënjëve merr vlera me shënjën e a-së dhe për të gjitha x Brenda rrënjëve merr vlera me shënjën e kundërt të a-së.
Në qoftë se D=0 trinomi për çdo x të ndryshëm nga rrënja merr vlera me shënjën e a-së.
Nëse D<0 trinomi për të gjitha x-et merr vlera me shënjën e a-së.

Hapat që ndiqen për studimin e shënjës së trinomit janë:

Trinomi barazohet me zero.
Gjejmë rrënjët e ekuacionit të formuar.
Ndërtohet tabela e studimit të shënjës së trinomit.

Shembull 1

Të studiohet shënja e trinomit $\displaystyle 2{{x}^{2}}-5x+2=0$

Zgjidhje

Në fillim barazojmë trinomin me zero:

$\displaystyle {{x}^{2}}-2x+1=0$ .

Zgjidhim ekuacionin. Gjejmë dallorin:

$\displaystyle D=25-4\cdot 2\cdot 2=9$

$\displaystyle _{1}{{x}_{2}}=\frac{5\pm 3}{4}$ , pra $\displaystyle {{x}_{1}}=\frac{1}{2}$ dhe $\displaystyle {{x}_{1}}=2$ .

Ndërtojmë tabelën:

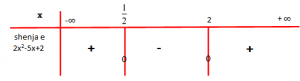
Tabela tregon se për $\displaystyle x\in \left] -\infty ,\frac{1}{2} \right[\cup \left] 2,+\infty \right[$ trinomi merr vlera positive.

Për $\displaystyle x\in \left] \frac{1}{2},2 \right[$ trinomi merr vlera negative dhe për $\displaystyle x\in \left\{ \frac{1}{2},2 \right\}$ trinomi merr vlerën zero.