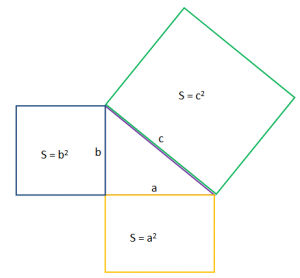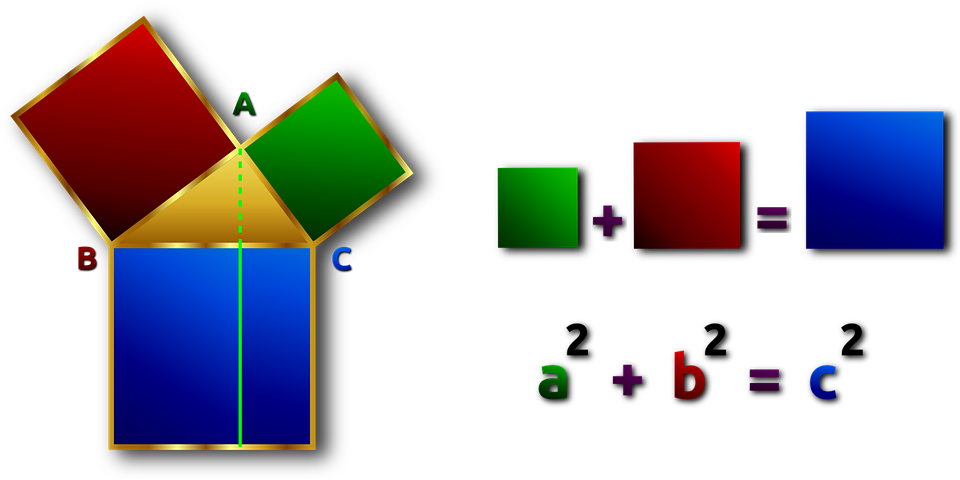
Teorema e Pitagores | Matematika

Teorema e Pitagores thotë: “Sipërfaqja e katrorit të ndërtuar mbi hipotenuzë është e barabartë me shumën e sipërfaqeve të ndërtuara mbi katete”.

Ndryshe shprehet: “Katrori i hipotenuzës është i barabartë me shumën e katrorëve të kateteve”.

Ky është një ilustrim nga teorema e Pitagores.

Me formulë, teorema e Pitagores shkruhet kështu:

$\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}$ , ku hipotenuza c është brinja më e madhe e trekëndëshit kënddrejt, ndërsa a dhe b janë katetet e tij.

Shembull 1

Jepet hipotenuza 10 cm dhe njëri katet 6 cm. Gjeni katetin tjetër.

Zgjidhje

Nga teorema e Pitagores, shkruajmë:

$\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}$

Veçojmë katetin b:

$\displaystyle {{b}^{2}}={{c}^{2}}-{{a}^{2}}$

$\displaystyle {{b}^{2}}={{10}^{2}}-{{6}^{2}}$

$\displaystyle {{b}^{2}}=100-36=64$

$\displaystyle b=\sqrt{64}=8cm$

Teorema e anasjelltë e Pitagores

Teorema e Pitagores mund të formulohet edhe kështu: “Nëse në një trekëndesh njëri kënd është i drejt, atëherë katrori i brinjës përballë tij është i barabartë me shumën e katrorëve të dy brinjëve të tjera”.

Teorema e anasjelltë është gjithashtu teoremë.
Ajo formulohet kështu: “Nëse në një trekëndësh, katrori i një brinje është i barabartë me shumën e katrorëve të dy brinjëve të tjera, atëherë këndi përballë kësaj brinje është i drejt”.

Shembull 1

Kemi të dhënë trekëndëshin me brinjë 3 cm, 4 cm dhe 5 cm.
Vërtetoni që ky trekëndësh është kënddrejt.

Zgjidhje

Për të kontrolluar nëse një trekëndësh është kënddrejt, do të zbatojmë teoremën e anasjelltë të Pitagorës.

Brinja me gjatësi 5 cm është brinja më e madhe, ndaj katrorin e saj do ta krahasojmë me shumën e katrorëve të dy brinjëve të tjera. Do të kemi:

$\displaystyle {{5}^{2}}={{3}^{2}}+{{4}^{2}}$

$\displaystyle 25=9+16$

$\displaystyle 25=25$

Identiteti është i vërtetë.

Nga teorema e anasjelltë , do të kemi që trekëndëshi me brinjë 3 cm, 4 cm dhe 5 cm është trekëndësh kënddrejt.

Shembull 2

Gjeni hipotenuzën e trekëndëshit kënddrejt nëse kemi të dhënë katetet 5 cm dhe 7 cm.

Zgjidhje

Nga teorema e Pitagores do të kemi:

$\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}$

$\displaystyle {{c}^{2}}={{5}^{2}}+{{7}^{2}}$

$\displaystyle {{c}^{2}}=25+49=74$

$\displaystyle c=\sqrt{74}~cm$ .

Figura e Pitagores

Statuja e Pitagores

Rreth viteve 600 para lindjes Eres se Re, në Greqinë Antike ka jetuar një njeri vërtet i jashtëzakonshëm i quajtur PITAGORA, i cili ka tentuar që të vërtetojë ekzistimin e të gjitha gjërave në Univers përmes harmonisë së përsosur të veprimit hyjnor të numrave. Jo vetëm që konsiderohej si themelues dhe baba i njohurisë mbi analizën e veprimit të numrave në natyrë- Numerologjia, por ishte dhe mbetej mistiku, okulisti, matematikani dhe filozofi më i madh i të gjitha kohërave.

Që në fillim duhet konstatuar se, shumë mësime të Pitagorës, edhe sot e kësaj dite konsiderohen si fshehtësi e madhe dhe se të gjitha shkathtësitë dhe praktikat okuliste të Perëndimit, burojnë nga mistika pitagoriane. Pesëdhjetë e katër vitet më të frytshme të jetës i ka kaluar në Egjipt. Persi, Indi dhe në vendet tjera të Lindjes, vende këto që atëbotë, konsideroheshin si qendrat më të mëdha të dijes, urtësisë mistike dhe mendimit filozofik të mbarë botës.

Shembull 1

Zgjidhje

Teorema e Pitagores mund të formulohet edhe kështu: “Nëse në një trekëndesh njëri kënd është i drejt, atëherë katrori i brinjës përballë tij është i barabartë me shumën e katrorëve të dy brinjëve të tjera”.

Shembull 1

Zgjidhje

Shembull 2

Zgjidhje

Figura e Pitagores

Postime te ngjashme: