
Sisteme inekuacionesh te fuqise se pare me nje ndryshore
Përkufizim: “Zgjidhje e sistemit të inekuacioneve me një ndryshore quhet çdo vlerë e ndryshores që është zgjidhje për secilin nga inekuacionet e sistemit”.
Për të zgjidhur një system dy inekuacionesh në R veprojmë kështu:
- Zgjidhim inekuacionin e parë, pra gjejmë bashkësinë
të zgjidhjeve të tij.
- Zgjidhim inekuacionin e dytë, pra gjejmë bashkësinë
të zgjidhjeve të tij.
- Gjejmë prerjen
Çdo zgjidhje e sistemit është zgjidhje e përbashkët e të dy inekuacioneve, pra i përket bashkësisë dhe bashkësisë
. Si rrjedhim ajo i përket prerjes
.
Anasjelltas: “Çdo element i prerjes është zgjidhje e sistemit”.
Përfundim: “Bashkësia e zgjidhjeve të sistemit është prerja ”.
Shembull 1
Të zgjidhet inekuacioni
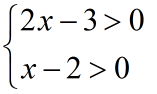
Zgjidhje
- Zgjidhim inekuacionin
.
Pra,
- Zgjidhim inekuacionin
Pra,
Gjejmë :
Pra, zgjidhja e sistemit është intervali .
Inekuacione të dyfishtë
Inekuacioni i dyfishtë përfaqëson sistemin e inekuacioneve:
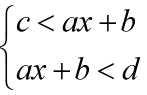
Për këtë arsye zgjidhja e inekuacioneve të dyfishtë mund të bëhet si ajo e sistemeve të zakonshëm. Por për zgjidhjen e inekuacioneve të dyfishtë mund të përdoret edhe një mënyrë e veçantë.
Shembull 2
Të zgjidhjet në dy mënyra inekuacioni i dyfishtë
Zgjidhje
Mënyra e parë: Ky inekuacion i dyfishtë përfaqëson sistemin
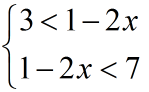
dhe zgjidhjet në mënyrën e njohur.
Mënyra e dytë: Përpiqemi të shfaqim në gjymtyrën e mesit (1-2x) vetem x-in.
(u zbresim të tre gjymtyrëve -1)
(shumëzojmë të tre gjymtyrët me -1)
(pjestojmë me 2 te tre gjymtyrët)
Përfundim: Bashkësia e zgjidhjeve të inekuacionit të dyfishtë është

