
Trekendeshat dhe
quhen te ngjashem, nëse këndet i kanë përkatësisht kongruente dhe brinjët homologe të përpjesshme.
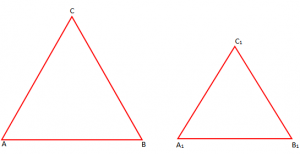
Shkruajmë:
;
;
.
.
Numri k quhet koeficient i ngjashmerisë.
Teoremë 1: “Raporti i sipërfaqeve të trekëndëshave të ngjashëm është i barabartë me katrorin e koeficientit të ngjashmërisë”.
Teoremë 2: “Raporti i perimetrave të trekëndëshave të ngjashëm është i barabartë me koeficientin e ngjashmërisë”.
Rasti i parë i ngjashmërisë së trekëndëshave
Teoremë: “Në qoftë se dy kënde të njërit trekëndësh janë përkatësisht kongruentë me dy kënde të trekëndëshit tjetër, atëherë trekëndëshat janë të ngjashem”.

Pra, në qoftë se dhe
, atëherë trekëndëshat
dhe
janë të ngjashem.
Rasti i dytë i ngjashmërisë së trekëndëshave
Teoremë: “Në qoftë se dy brinjë të njërit trekëndësh janë të përpjesshme me dy brinjë të trekëndëshit tjetër dhe këndet që formohenprej tyre janë përkatësisht kongruentë , atëherë trekëndëshat janë të ngjashëm”.

Pra, në qoftë se  dhe
dhe  , atëherë trekëndëshat
, atëherë trekëndëshat ![Rendered by QuickLaTeX.com \displaystyle ABC]() dhe
dhe  janë të ngjashem.
janë të ngjashem.
Rasti i tretë i ngjashmërisë së trekëndëshave
Teoremë: “Në qoftë se tri brinjët e një trekëndëshi janë të përpjesshme me tri brinjët e një trekëndëshi tjetër, atëherë këta trekëndësha janë të ngjashem”.

Pra, në qoftë se , atëherë trekëndëshat
dhe
janë të ngjashem.
Vija e mesme e trekëndëshit
Përkufizim: “Vijë e mesme e trekëndëshit quhet segmenti që bashkon meset e dy brinjëve të tij”.
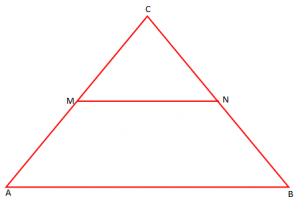
[MN] vijë e mesme e trekëndëshit ABC, pra [AM] = [MC] dhe [BN] = [NC].
Teoremë: “Vija e mesme e trekëndëshit është paralele me njërën brinjë të tij dhe e barabartë me gjysmën e saj”.
Pra, dhe
.

