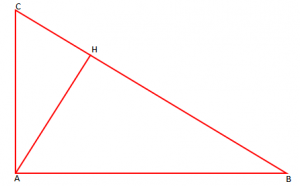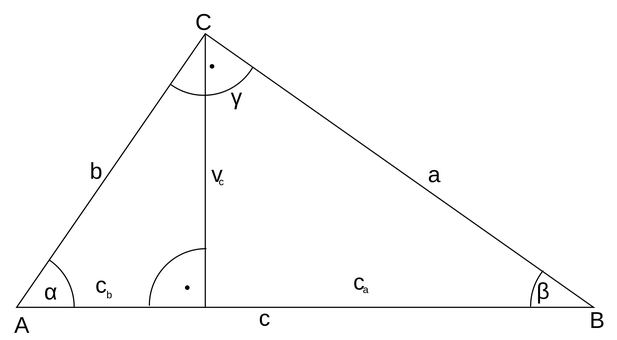
Teoremat e Euklidit | Teorema e pare dhe e dyte e Euklidit

Teorema e Euklidit: Kemi trekëndëshin kënddrejtë. Nga kulmi i këndit të drejtë ndërtojmë lartësinë AH mbi hipotenuzë.

teorema e euklidit

Segmentet [CH] dhe [BH] janë projeksionet e kateteve mbi hipotenuzën BC.

Trekëndëshat ABC dhe ABH janë të ngjashëm sepse kanë një kend të ngushtë (kendi B) të barabartë, ndaj do të kemi:

$\displaystyle \frac{AH}{CH}=\frac{BH}{AH}$ , nga ku $\displaystyle {{[AH]}^{2}}=CH\cdot BH$ .

Kështu kemi vërtetuar teoremën e parë të Euklidit.

Teorema e parë e Euklidit: “Në trekëndëshin kënddrejtë, lartësia e hequr nga kulmi i këndit të drejtë është e mesme e përpjesshme ndërmjet projeksioneve të kateteve mbi hipotenuzë”.

Trekëndëshat ABC dhe AHC janë gjithashtu të ngjashëm, për të njëjtën arsye si tek rasti më lart. Do të kemi:

$\displaystyle \frac{AC}{CH}=\frac{BC}{AC}$ nga ku $\displaystyle {{[AC]}^{2}}=BC\cdot CH$ .

Ky barazim shpreh teoremën e dytë të Euklidit.

Teorema e dytë e Euklidit: “Në trekëndëshin kënddrejtë, çdo katet është i mesëm i përpjesshëm ndërmjet hipotenuzës dhe projeksionit të tij mbi hipotenuzë”.

Shembull 1

Në trekëndëshin kënddrejtë ABC, jepen katetet AC = 6 cm dhe AB = 8 cm. Gjeni hipotenuzën, projeksionet e kateteve si dhe lartësinë mbi hipotenuzë.

Zgjidhje

Gjejmë hipotenuzën:

Nga teorema e Pitagorës, kemi:

$\displaystyle {{\left( BC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( AC \right)}^{2}}$ .

$\displaystyle {{\left( BC \right)}^{2}}={{8}^{2}}+{{6}^{2}}=64+36=100$

$\displaystyle BC=\sqrt{100}=10~cm$ .

Gjejmë projeksionet e kateteve.

Nga teorema e dytë e Euklidit: “Në trekëndëshin kënddrejtë, çdo katet është i mesëm i përpjesshëm ndërmjet hipotenuzës dhe projeksionit të tij mbi hipotenuzë”, do të kemi:

$\displaystyle {{\left( AC \right)}^{2}}=BC\cdot CH$