Kufizueshmeria e funksionit

Ndërtojmë në të njëjtin grafik funksionet ,  dhe funksionin , .

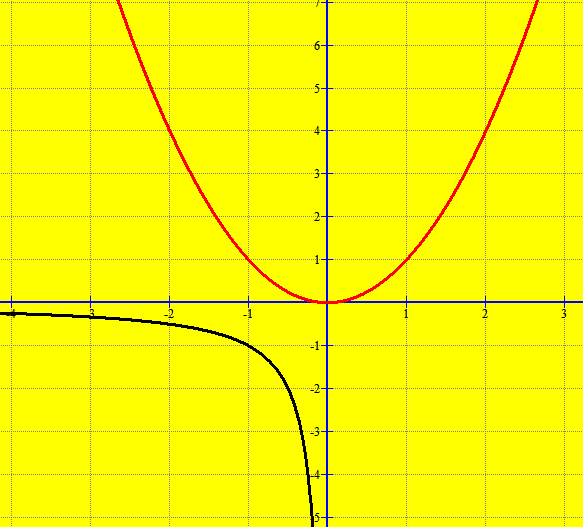
Siç duket nga grafiku, funksioni merr vlera më të vogla se zero. Në këtë rast funksioni quhet i kufizuar nga lart.

Përkufizim 1: “Funksioni numerik f quhet i kufizuar nga lart në bashkësinë A nëse ekziston një numër M i tillë që për çdo ”.

Në këtë rast, grafiku i funksionit f ndodhet nën drejtëzën .

Për funksionin , vlerat e funksionit rriten pa kufi, nuk ka numër për të cilin të mos gjenden vlera të funksionit akoma më të mëdha.

Mund të ndodh që vlerat e një funksioni numerik f, të jenë më të mëdha se një numër i caktuar. Në këtë rast funksioni f quhet i kufizuar nga poshtë.

Përkufizim 2: “Funksioni numerik f quhet i kufizuar nga poshtë në bashkësinë A, nëse ekziston një numër m i tillë që për çdo ”.

Në këtë rast, grafiku i funksionit f ndodhet mbi drejtëzën .

Përkufizim 3: “Funksioni numerik f quhet i kufizuar në bashkësinë A, nëse ai është i kufizuar nga lart dhe nga poshtë në këtë bashkësi”.

Studimi i variacionit

Të studiosh variacionin e një funksioni numerik do të thotë të studiosh si ndryshojnë vlerat e tij me ndryshimin e vlerave të x-it. Për studimin e variacionit ndjekim këto hapa:

1. Gjejmë bashkësinë e përcaktimit.
2. Studiojmë monotonin e funksionit, pra pjesët ku ai është rritës osë zbritës.
3. Studiojmë kufizueshmërin e funksionit.
4. Gjejmë, nëse ekzistojnë, vlerën më të madhe dhe më të vogël të funksionit. Gjejmë bashkësinë e vlerave të funksionit. Gjejmë pikën ku grafiku pret boshtet koordinative.
5. Studimi përmblidhet në një tabelë që quhet tabelë e variacionit.