
Llogaritja e siperfaqeve te figurave plane
Metodat e gjeometrisë elementare që ne njohim, japin kuptimin e sipërfaqes së figurës dhe mundësinë e llogaritjes së saj për një klasë pothuajse të ngushtë figurash plane, siç janë trekëndëshi, katërkëndëshi etj.
Problem i përgjithshëm gjeometrik i përcaktimit të figurës plane të kufizuar nga një vijë e çfarëdoshme u bë e mundur të zgjidhet me anë të njehsimit integral.
Rasti i parë që do shohim është figura plane e quajtur trapez vijëpërkulur.
Le të jepet funksioni i vazhdueshëm dhe pozitiv në
.
Figura plane e kufizuar nga boshti i abshisave Ox, dy drejtëza me ekuacione dhe
dhe grafiku i funksionit
në segmentin
quhet trapez vijëpërkulur.
Do të pranojmë pa vërtetim që sipërfaqja e këtij trapezi jepet me formulën:
.
Ushtrimi 1
Të llogaritet sipërfaqja e figurave plane të kufizuara nga vijat:
a) ;
;
;
b) ;
;
;
c) ;
;
Zgjidhje
a)
b)
c)
Rasti i përgjithshëm
Figura plane jepet nga vijat ;
dhe drejtëzat
dhe
.
Në të gjitha rastet, sipërfaqja e figurave të vijëzuara jepet me formulën:
Ushtrimi 2
Të gjendet sipërfaqja e figurave plane të kufizuara nga vijat:
a) dhe
b) dhe
Zgjidhje
a) Për të gjetur kufijtë e integrimit, zgjidhim sistemin:
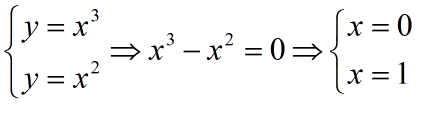
Pra, do të kemi:
b) Gjejmë kufijtë e integrimit:
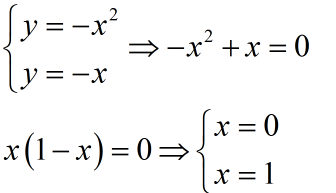
Pra, do të kemi:

