Çiftesia e funksionit. Funksioni periodik | Matematika

Çiftesia e funksionit

Përkufizim 1: “Funksioni f quhet çift në qoftë se për çdo $\displaystyle x\in R$ plotësohen njëherësh dy kushte: $\displaystyle \left( -x \right)\in E$ dhe $\displaystyle f\left( -x \right)=f\left( x \right)$ ”.

Përkufizim 2: “Funksioni f quhet tek në qoftë se për çdo $\displaystyle x\in R$ plotësohen njëherësh dy kushte: $\displaystyle -x\in E$ dhe $\displaystyle f\left( -x \right)=-f\left( x \right)$ ”.

Për shembull funksionet $\displaystyle y={{x}^{2}}$ dhe $\displaystyle y=\cos x$ gezojnë vetitë:

$\displaystyle \left( -{{x}^{2}} \right)={{x}^{2}}$ dhe $\displaystyle \cos \left( -x \right)=\cos x$ për çdo $\displaystyle x\in R$ d.m.th $\displaystyle f\left( -x \right)=f\left( x \right)$ , për çdo $\displaystyle x\in R$ .

Funksionet $\displaystyle y={{x}^{3}}$ dhe $\displaystyle y=\sin x$ gëzojnë vetitë:

$\displaystyle {{\left( -x \right)}^{3}}=-{{x}^{3}}$ dhe $\displaystyle \sin \left( -x \right)=-\sin x$ , d.m.th $\displaystyle f\left( -x \right)=-f\left( x \right)$ .

Teoremë 1: Grafiku i funksionit çift ka si bosht simetrie boshtin oy.

Për shembull marrim funksionin $\displaystyle y={{x}^{2}}$ .

Ndërtojmë grafikun:

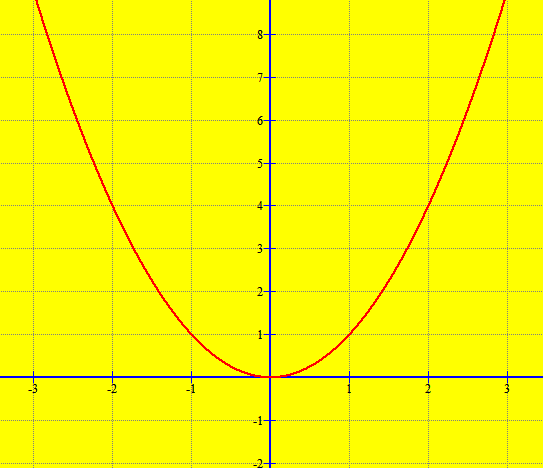
Siç duket nga grafiku, funksioni $\displaystyle y={{x}^{2}}$ ka si bosht simetrie boshtin oy.

Teoremë 2: Grafiku i funksionit tek ka si bosht simetrie origjinën e koordinatave.

Për shembull, marrim funksionin $\displaystyle y={{x}^{3}}$ .

Ndërtojmë grafikun:

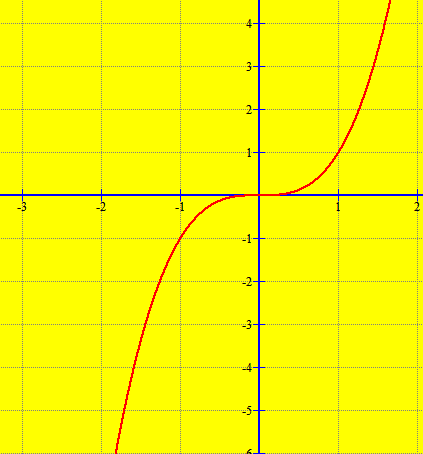
Siç duket nga grafiku, funksioni $\displaystyle y={{x}^{3}}$ ka si qendër simetrie qendrën e koordinatave.

Metodë: Nëse dihet që funksioni numerik f, me bashkësi përcaktimi R, është çift apo tek, gjatë studimit të tij, për të thjeshtuar punë, mund të shqyrtojmë vetëm pjesën jo negative të bashkësisë së përcaktimit. Nga vetitë e f në këtë bashkësi mund të nxirren të gjithë vetitë e f në E.

Teoremë: Nëse funksionet numerike f,g janë funksione çift në bashkësinë A, atëherë funksioni $\displaystyle S=f+g$ është funksion çift në A.

Funksionet periodike

Funksionet $\displaystyle y=\sin x$ dhe $\displaystyle y=\cos x$ , $\displaystyle y=tgx$ janë funksione periodike. Le të jetë f një funksion numerik me bashkësi përcaktimi E.

Përkufizim: Funksioni f quhet periodik në qoftë se ekziston të paktën një numër $\displaystyle a\ne 0$ , i tillë që për çdo $\displaystyle x\in E$ , të kemi $\displaystyle \left( x-a \right)\in E$ , $\displaystyle \left( x+a \right)\in E$ dhe $\displaystyle f\left( x+a \right)=f\left( x \right)$ .

Në qoftë se një numër i tillë a ekziston, ai nuk është i vetëm. Këtë veti e gëzojnë edhe të gjithë numrat e trajtës $\displaystyle k\cdot a$ ku $\displaystyle k\in Z$ .

Pra, nga kjo rrjedh:

$\displaystyle f\left( x+k\cdot a \right)=f\left( x \right)$ , për çdo $\displaystyle x\in E$ .

Për shembull $\displaystyle f\left( x+3a \right)=f\left( x+a+a \right)=f\left( x \right)$ .

Në rast se funksioni f është periodik, numri më i vogël pozitiv a, i tillë që $\displaystyle f\left( x+a \right)=f\left( x \right)$ , për çdo $\displaystyle x\in E$ , quhet period e funksionit.

Perioda e funksioneve $\displaystyle y=\sin x$ dhe $\displaystyle y=\cos x$ është $\displaystyle 2\pi$ , ndërsa perioda e funksionit $\displaystyle y=tgx$ është π.

Grafiku i funksionit periodik

Në përgjithësi, grafiku i funksionit periodik, “përsërit veten” pas segmentesh me gjatësi sa perioda.

Metodë: Për të ndërtuar grafikun e funksionit periodik me periodë T, veprojmë kështu:

Zgjedhim një segment me gjatësi sa perioda, p.sh $\displaystyle \left[ 0,T \right]$ , ose $\displaystyle \left[ -\frac{T}{2},\frac{T}{2} \right]$
Ndërtojmë pjesën përkatëse $\displaystyle l$ të grafikut (për x nga ky segment).
Bëjmë zvhendosjen paralele të $\displaystyle l$ me secilin nga vektorët e trajtës $\displaystyle k\cdot T\cdot \vec{i}$ (ku $\displaystyle k\in Z$ dhe $\displaystyle {\vec{i}}$ është vektori njësi i bushtit ox).