
Krahasimi i funksioneve numerike
Përkufizim: Themi se funksioni f është më i madh se funksioni g në bashkësinë A,nëse për çdo është i vërtetë mosbarazimi
Në këtë rast themi gjithashtu se funksioni f është më i vogël së funksioni g në bashkësinë A.
Shënojmë ose
.
Mosbarazimi është i jëvlershëm me
.
Në rastin kur , shkruajmë
. Metodë: Kur funksionet f,g janë dhënë me formula, për t’i krahasuar ato mjafton të studiojmë shenjën e diferencës.
Shembull 1
Janë dhënë funksionet dhe
.
a) Të krahasohen këta funksione në R.
b) Të gjendet bashkësia më e gjerë në të cilën f
Zgjidhje
a) Kemi dhe
.
Diferenca është
.
.
Zgjidhim ekuacionin e fuqisë së dytë me një ndryshore:
.
.
Studiojmë shenjën e trinomit:
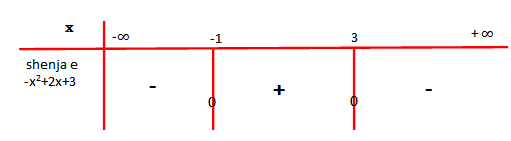
Për kemi
, prandaj f>g.
Për dhe
, kemi
, prandaj fb) Bashkësia më e gjerë ku f
Mbledhja e dy funksioneve numerike
Le të jenë f,g dy funksione numerike të përcaktuara përkatësisht në bashkësitë dhe
.
Shënojmë me D prerjen e dy bashkësive dhe
.
.
Për çdo vlerë të , ekziston një vlerë e vetme f(x) e funksionit f dhe një vlerë e vetme e g(x) e funksionit g.
Duke i çiftuar vlerës së x shumën , marrim një funksion të ri të përcaktuar në D. Ky funksion i ri quhet shumë e funksioneve f,g dhe shënohet f+g.
Shuma f+g e funksioneve f,g është funksion i përcaktuar në D,i dhënë kështu:
ose
.
Fakti që vlera e funksionit f+g në pikën x është sa shuma e vlerave të funksioneve numerike f,g në këtë pikë, shënohet kështu:
.
Shembull 1
Gjeni bashkësinë e përcaktimit dhe shumën f+g për funksionet:
a) Le të kemi funksionet f,g me bashkësi përcaktimi R.
dhe
.
b) Le të kemi funksionet:
me bashkësi përcaktimi
me bashkësi përcaktimi
.
Zgjidhje
a) Bashkësia e përcaktimit të shumës f+g është përsëri bashkësia e numrave real sepse dhe shuma f+g shkruhet me formulën
.
b) Bashkësia e përcaktimit e shumës f+g është:
.
Veprime të tjera me funksionet
Në mënyrë të ngjashme me përkufizimin e shumës jepen përkufizimet e prodhimit të dy funksioneve numerike f,g që shënohet , të herësit të funksionit f me funksionin g që shënohet
dhe të prodhimit të numrit real c me funksionin f që shënohet
.
Ndërtojmë tabelën për këto raste:
| Funksioni | Bashkësia e përcaktimit | Mënyra e çiftimit |

