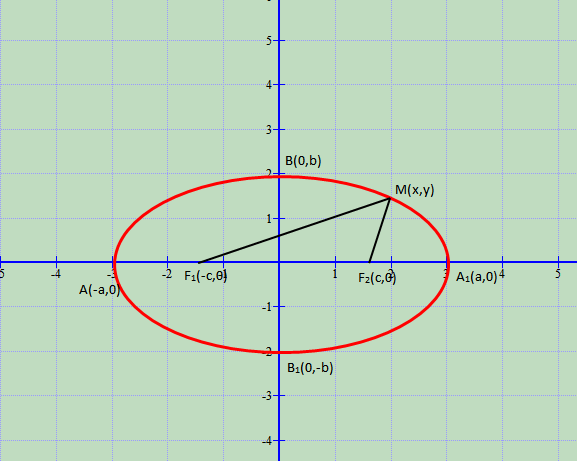
Elipsi dhe ekuacioni i tij
Elipsi është bashkësia e pikave të planit, shuma e largesave të të cilave nga dy pika të dhëna të planit është madhësi konstante.
Për të nxjerrë ekuacionin e elipsit, zgjedhim si bosht të abshisave drejtëzën që bashkon dy vatrat, ndërsa origjinën e koordinatave e caktojmë në mesin e e segmentit që bashkon vatrat.
Shënojmë me 2c largesën ndërmjet vatrave dhe
. Do të kemi
dhe
.
Shënojmë një pikë çfarëdo të elipsit. Segmentet
dhe
quhen rreze vatrore të pikës M. gjatësitë e tyre i shënojmë
dhe
.
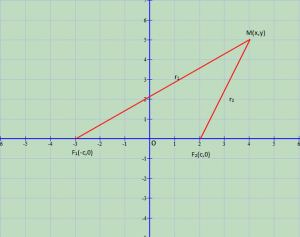
Kemi dhe
.
Sipas përkufizimit, shuma është madhësi konstante. E shënojmë atë me
.
Pra, kemi ose
.
Ky është ekuacioni i elipsit.
Duke bërë disa shndërrime identike, arrijmë në përfundimin:
ku
, i cili quhet ekuacioni më i thjeshtë i elipsit.
Shembull 1
Të gjendet ekuacioni i elipsit duke ditur se largesa ndërmjet vatrave është është 10 cm, ndërsa shuma e e rrezeve vatrore është 12 cm.
Zgjidhje
Largesa ndërmjet vatrave është 2c, pra ;
.
Shuma e e rrezeve vatrore është 2a, pra ;
.
Nga formula gjejmë b:
.
.
Pra, ekuacioni i elipsit është:
Forma e elipsit
- Simetria
Boshtet koordinative janë boshte simetrie për elipsin, ndërsa origjina e koordinatave është qendër simetrie e tij. Kjo quhet qendër e elipsit.
- Pikat e prerjes me boshtet
Duke marr , kemi
, pra
. Pikat
dhe
janë pikat e prerjes së elipsit me boshtin e abshisave.
Duke marr , kemi
, pra
. Pikat
dhe
janë pikat e prerjes së elipsit me boshtin e ordinatave.
Segmenti quhet boshti i madh, ndërsa segmenti
quhet boshti i vogël i elipsit,.
Madhësitë a dhe b quhen gjysmëboshti i madh dhe gjysmëboshti i vogël i elipsit.
- Zona e vendosjes
Elipsi ndodhet Brenda brezit të kufizuar nga drejtëzat  dhe
dhe  .
.
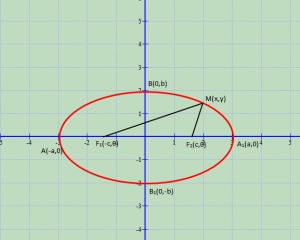
- Forma e elipsit
Me rritjen e x nga zero në a, y zvogëlohet nga b në zero. Në këtë mënyrë, forma e elipsit është:
Ushtrimi 1
Shkruani ekuacionin e elipsit kur jepet:
a) dhe
b) Gjysmëboshtet janë 5 dhe 3.
c) Boshtet janë 8 dhe 4
d) Gjysmëboshti i vogël është 2 dhe largesa ndërmjet vatrave është 8.
Zgjidhje
a) Në këtë rast ekuacioni do të jetë:
b) Kurt themi që gjysmëboshtet janë 5 dhe 3, do të thotë që dhe
, pra ekuacioni i elipsit do të jetë:
c) Boshtet janë 8 dhe 4, pra dhe
. Ekuacioni i elipsit do të jetë:
d) Gjysmëboshti i vogël është 2 dhe largesa ndërmjet vatrave është 8, pra dhe
.
Nga formula gjejmë a:
.
Ekuacioni i elipsit do të jetë:

