Ekstremumet e funksionit | Matematika 12

Ekstremumet e funksionit

Teorema 1: Në qoftë se funksioni f është i derivueshëm në intervalin $\displaystyle \left] a-r,a+r \right[$ dhe ka derivat pozitiv në çdo pikë të intervalit $\displaystyle \left] a-r,a \right[$ dhe derivat negativ në çdo pikë të intervalit $\displaystyle \left] a,a+r \right[$ , atëherë ky funksion ka maksimum për $\displaystyle x=a$ .

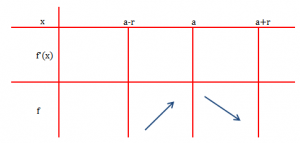
Në figurën më sipër tregohet skematikisht kushti dhe përfundimi i kësaj teoreme.

Teorema 2: Në qoftë se funksioni f është i derivueshëm në intervalin $\displaystyle \left] a-r,a+r \right[$ dhe ka derivate negativ në çdo pikë të intervalit $\displaystyle \left] a-r,a \right[$ dhe derivate pozitiv në çdo pikë të intervalit $\displaystyle \left] a,a+r \right[$ , atëherë ky funksion ka minimum për $\displaystyle x=a$ .

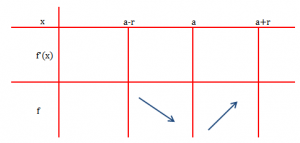
Në figurën më sipër tregohet skematikisht kushti dhe përfundimi i kësaj teoreme.

Shembull 1

Të gjendet ekstremumet e funksionit $\displaystyle y=2x-{{x}^{2}}$

Zgjidhje

Për çdo $\displaystyle x\in R$ kemi $\displaystyle y'=2-2x$ .

Studiojmë shenjën e derivatit:

$\displaystyle 2-2x=0$

$\displaystyle x=1$

Në këtë rast a=2.

Bëjmë studimin e shënjës:

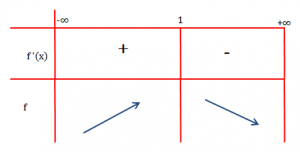
Pra, siç duket, pika x=1 është maksimum për funksionin $\displaystyle y=2x-{{x}^{2}}$ .

Teorema 3: Në qoftë se funksioni f është i derivueshëm në intervalin $\displaystyle \left] a-r,a+r \right[$ dhe $\displaystyle f'\left( a \right)=0$ por $\displaystyle f'\left( x \right)$ ruan të njëjtën shenjë në të dyja intervalet $\displaystyle \left] a-r,a \right[$ dhe $\displaystyle \left] a,a+r \right[$ , atëherë ky funksion nuk ka ekstremum në pikën a.

Shembull 2

Gjeni ekstremumet e funksionit $\displaystyle y=\frac{1}{3}{{x}^{3}}-2{{x}^{2}}+3x-7$

Zgjidhje

Gjejmë derivatin:

$\displaystyle y'={{x}^{2}}-4x+3$

Barazojmë derivatin me zero dhe bëjmë studimin e shënjës:

$\displaystyle {{x}^{2}}-4x+3=0$

$\displaystyle D=16-12=4$

$\displaystyle _{1}{{x}_{2}}=\frac{4\pm \sqrt{4}}{2}$

$\displaystyle {{x}_{1}}=\frac{4-2}{2}=1$

$\displaystyle {{x}_{2}}=\frac{4+2}{2}=3$ .

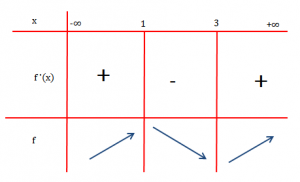
Ky funksion nuk ka ekstremum.

Teorema 4: Nëse funksioni në çdo pikë të intervalit të parë e të dytë dhe në pikën $\displaystyle a\in I$ kemi $\displaystyle f'\left( a \right)=0$ dhe $\displaystyle f''\left( a \right)\ne 0$ , atëherë ky funksion ka në pikën a ekstremum.

Ky ekstremum është maksimumm kur $\displaystyle f''\left( a \right)<0$ dhe minimum kur $\displaystyle f''\left( a \right)>0$ .

Shembull 3

Studioni monotoninë dhe gjeni ekstremumet e funksionit $\displaystyle y=2{{x}^{3}}-3{{x}^{2}}$

Zgjidhje

Gjejmë derivatin e parë:

$\displaystyle y'=6{{x}^{2}}-6x$

$\displaystyle y'=6x\left( x-1 \right)$

E barazojmë atë me zero:

$\displaystyle 6x\left( x-1 \right)=0$

Derivati ka zgjidhje $\displaystyle x=0$ ose $\displaystyle x=1$ .

Gjejmë derivatin e dytë dhe zëvëndësojmë vlerat që gjetëm:

$\displaystyle y''=12x-6$

$\displaystyle y''\left( 0 \right)=0-6=-6$

$\displaystyle y''\left( 1 \right)=12-6=6$ .

Pra, funksioni ka maksimum në pikën x=0 dhe minimum në pikën x=1.

Pra, do të kemi:

Funksioni është rritës në $\displaystyle \left] -\infty ,0 \right[$ dhe në $\displaystyle \left] 1,+\infty \right[$ dhe zbritës në $\displaystyle \left] 0,1 \right[$ .