Perimetri

Përkufizim: Perimetri i nje figure është shuma e gjatësive të të gjitha brinjëve të tij.

Për figurat që brinët e tyre s’kanë ndonjë cileësi të përbashkët, nuk kanë formulë për gjetjen e perimetrit të tyre. Përimetri i tyre gjendet duke matur gjatësitë e të gjitha brinjëve dhe duke i mbledhur ato.

Për perimetrat e figurave të rregullta (p.sh që i kanë gjitha brinjët të barabarta), ka formula.

Përkufizim: Shumëkëndësha barabrinjës quhen ata shumëkëndësha që i kanë të gjitha brinjët e barabarta (p.sh, rombi, katrori etj).

Nëse në një shumëkëndësh barabrinjës të rregullt shënojmë:

a–>gjatësia e brinjës së tij

n–>numri I brinjëve të shumëkëndëshit

P–>Perimetri I tij, atëherë do të kemi:

P = a ∙ n

Nga formula e përgjithshme e perimetrit të shumëkëndëshit barabrinjës, nxjerrim vacant formulat për katrorin, trekëndëshin barabrinjës dhe gjashtëkëndëshit barabrinjës:

1) Trekëndëshi barabrinjës:

P = 3 ∙ a

2) Katrori

P = 4 ∙ a

3) Gjashtëkëndëshi barabrinjës:

P = 6 ∙ a

Perimetri i rrethit

Formula e perimetrit të rrethit është:

P = 2 ∙ π ∙ r

Π – është një numër dhjetor i pafundëm, jo periodik dhe i përket numrave irracional.

Π shpreh raportin e perimetrit të rrethit me diametrin e tij.

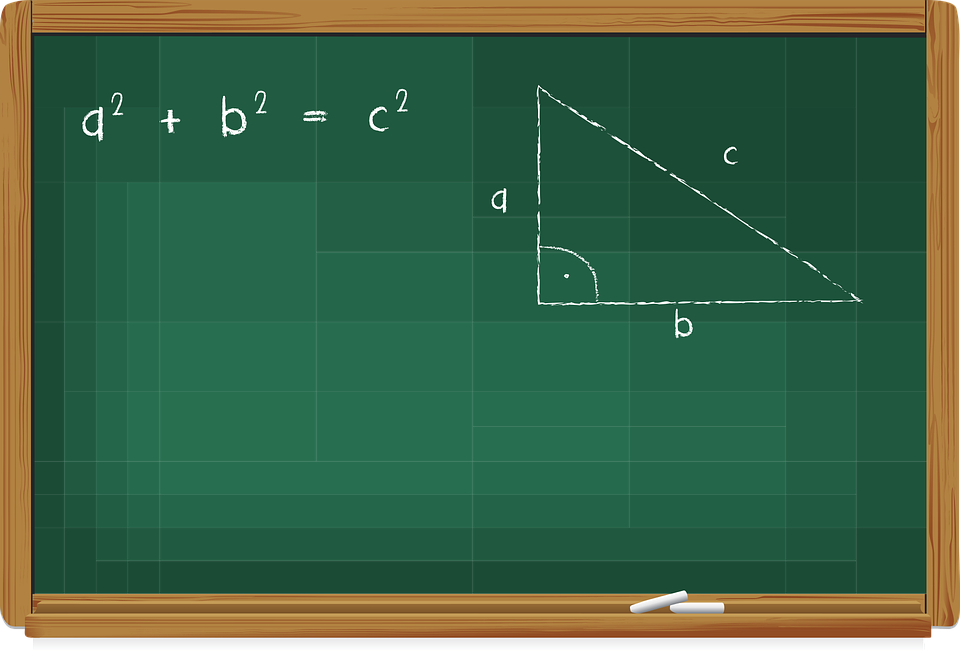
Pohimi i Pitagorës

Pohimi i pitagorës thotë: “Në një trekëndësh kënddrejt, katrori i ndërtuar mbi hipotenuzë është i barabartë shumën e katrorëve të ndërtuar mbi katete”.

Shohim figurën:

Ushtrime te zgjidhura dhe te pazgjidhura mbi perimetrin do ti gjeni duke klikuar ketu

Sipërfaqja

Sipërfaqja e qarkut

Përkufizim: Sipërfaqja e qarkut është e barabartë me prodhimin e numrit π me katrorin e rrezes.

Pra, shkruajmë:

$\displaystyle S=\pi \cdot {{r}^{2}}$

Shembull:

Gjeni sipërfaqen e qarkut me rreze 5 cm.

$\displaystyle S=\pi \cdot {{r}^{2}}$

$\displaystyle S=\pi \cdot {{5}^{2}}$

$\displaystyle S=25\pi c{{m}^{2}}$

Sipërfaqja e paralelogrameve

Formulën e gjetjës së sipërfaqes së paralelogramit e kemi mësuar në klasën e gjashtë, ku kemi:

S = b ∙ h

ku b është njëra brinjë dhe h është lartësia e ndërtuar mbi këtë brinjë.

Sipërfaqja e trapezit

Përkufizim: Sipërfaqja e trapezit gjendet duke shumëzuar shumën e bazave me lartësinë e trapezit dhe prodhimin e pjestojmë me 2.

Shkruajmë:

$\displaystyle S=\frac{(B+b)\cdot h}{2}$

Nga rrjedhimi i kësaj formule nxjerrim:

$\displaystyle h=\frac{2\cdot S}{B+b}$ dhe

$\displaystyle B+b=\frac{2\cdot S}{h}$

Ushtrime te zgjidhura dhe te pazgjidhura mbi perimetrin do ti gjeni duke klikuar ketu